Sign In Sign-Up

Welcome!

Close

Would you like to make this site your homepage? It's fast and easy...

Yes, Please make this my home page!

No Thanks

  Don't show this to me again.

Close

Angles between graphs

In many applications of the graph theory, especially of chemical ones, much interest has been paid to the problem of recognition of graphs - how to find if two graphs are equivalent or if they have at least a common subgraph.

Two graphs, G₁ and G₂ are called equivalent, if there exists a group of cyclic permutations S_n which transforms one graph into another

G₁ = P^TG₂P (1)

P represents all unit permutation matrices of the group. At least one from them should be effective.

In this paper, we will study the problem of the spectra of graph matrices, and therefore we will need another definition of the similarity, according to the definition of the relation of two vectors by the angle at which they cross.

Essentially, there are following main possibilities, how two graphs can be related:

1. Two graphs G₁ and G₂ are identical (collinear), if both their vertex and edge (arc) sets are identical.

2. Two graphs G₁ and G₂ are different, if their vertex and edge sets are different. But they can still be equivalent according to the definition (1).

3. The vertex and edge sets of two graphs G₁ and G₂ can have some common elements.

4. The vertex sets of two graphs G₁ and G₂ are identical. In this case their edge sets can be identical, as in the case (1), or they can have only some common elements or none common elements. The graph G₂ can be eventually the complement of the graph G_K1 of the graph G₁to the complete graph K or some of the subgraphs of G_K1.

We define the angle between two graphs G₁ and G₂ similarly as defined for two vectors

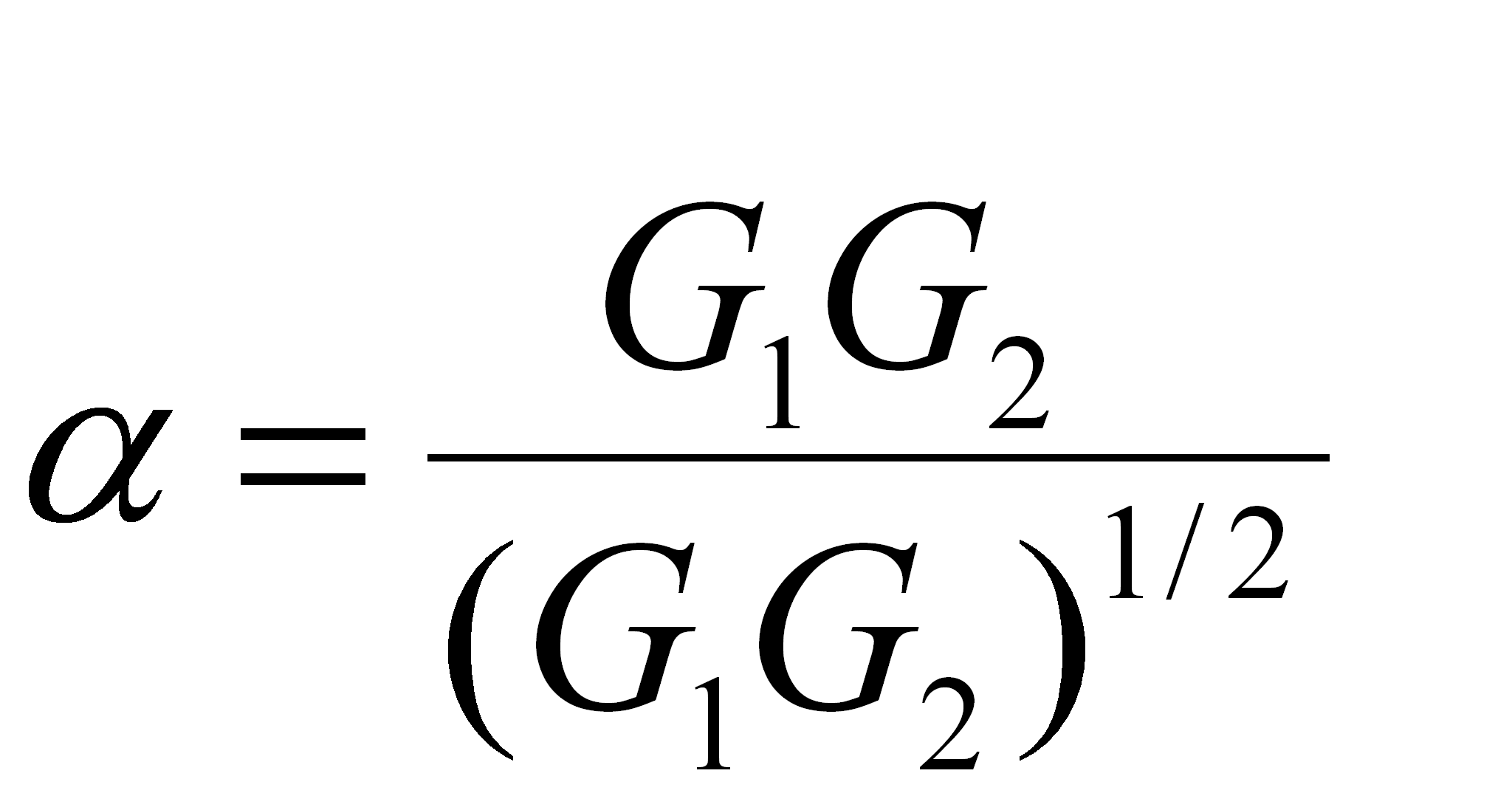(2)

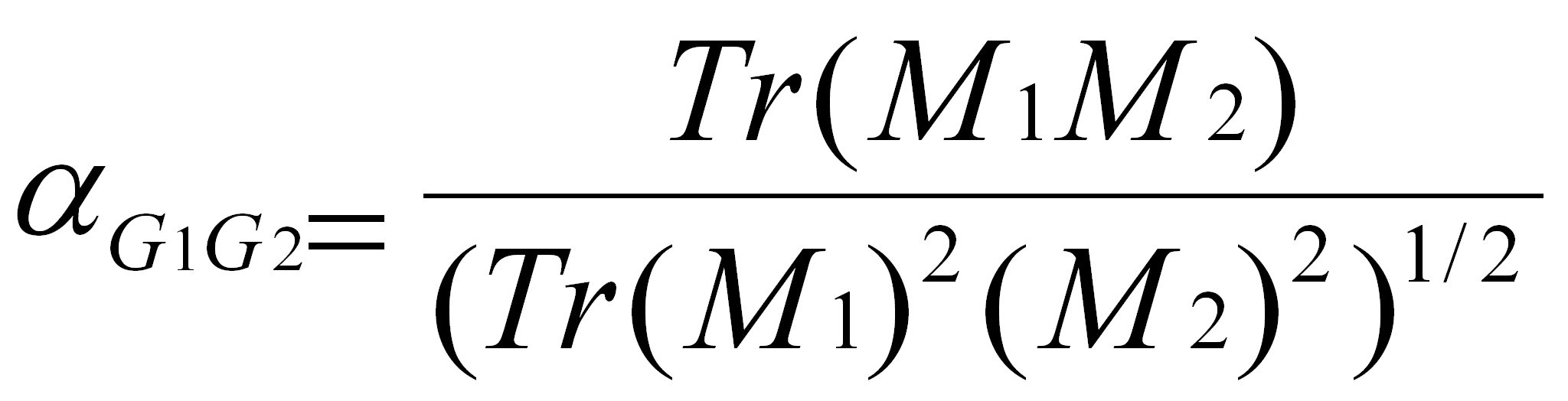
where Tr(M_j) is the trace of the matrix characterizing the graph G_j.

To clear the definition more, we must at first discuss the convention of multiplication of matrices.

In textbooks of the linear algebra, the multiplication of matrices of different formats is forbidden. Nevertheless, it is possible to add zero columns and rows to any matrix and to change its format.

If we try to multiply two matrices, both with different zero columns and rows (corresponding to different vertices), then in the product appear zero blocs with a great probability. It means that both matrix vectors are orthogonal. Nevertheless, the operation is possible, even if has no sense.

The definition of the graph angle will be applied to the Laplace-Kirchhoff matrices S^TS, where S^T is the transpose of the incidence matrix S of an oriented graph which rows are differences of two unit vectors (e_j - e_i) corresponding to the arc ij.

For example, two arcs with one common vertex form an angle with cos 1/4, 4 being the trace of (S^TS)².

Using the trace criterion, the linear chains L(4), obtained from the complete graph K (4), are arranged as follows

The first and the last chains are complementary, nevertheless, the cosine is 0.5.

If the numbering is fixed, the head and tail readings are equivalent.

There exists another possibility for evaluation of proximity of permutations, the Spearman coefficient S.

It consider the permutation as a vector and evaluates the squared Euclidean distance. This criterion gives

Here, the opposite readings are complementary, the sum of their coefficients is always 1.

Discussion

According to the proposed definition of the graph angle, two graphs are orthogonal in the space of vertices only if they have no common vertices. Such graphs must be orthogonal even in the space of arcs, because they can not have any common arcs. Two graphs with common vertices can still be orthogonal in the space of arcs, if they have no common arcs.

This orthogonality seems to have little common with the corresponding permutations of the parent graph.