|
|
|
ABC of
Entropy
Research Institute of Macromolecular
Chemistry, 656 49
There exist thousands of
publications about the entropy and despite of it Peres (1) and Weinberg (2)
could not agree about its definition in the recent polemics about the
application of the second law of thermodynamics in quantum mechanics.
In this journal same papers
appeared recently (3-6) devoted to the problem.
Actually, the problem must be
divided into two parts, the problem of the mathematical formula
H = -S pklog pk /1/
And the problem of physical
entropy S. We try to clear the problem of the function H on elementary level.
The only difficulty to be overcome is the notion of the n-dimensional space,
but it can be explained with the alphabet.
Our explanation follows exactly
Boltzmann (7) and Shannon (8), where the infinite model was abandoned and
virtual symbols (not occurring in an actual text) allowed.
A. On the
plain of the constant energy
The Bolzmann’s example was
simply an isolated system of 7 particles with 7 quanta of energy. We should
start with the 3 dimensional phase space, where the coordinates of all
particles are registered at one moment, take two following moments and find
their difference. We had 6.7 = 42 coordinates. Instead we use 7 dimensional
Euclidean space in which all vectors are orthogonal and draw all possible
combinations having the constant sum S mj = 7.
Only points which coordinates are natural numbers (zero including) appear as
the possible solution of the distribution problem. They lie on the plane
orthogonal with the positive cone and form the simplex. With this simplex are
differences of our 7- dimensional phase space isomorphic.
The problem was simplified but
not for us, because we are 3-dimensional animals and our abilities to
understand higher dimensional spaces are limited. We must analyze such simplex
at first. For it we divide the simplex into orbits
|
7000000 |
|
|
|
|
|
|
|
|
610000 |
|
|
|
|
|
|
|
520000 |
5110000 |
|
|
|
|
|
|
430000 |
4210000 |
4111000 |
|
|
|
|
|
|
3310000 |
3211000 |
3111100 |
|
|
|
3220000 |
||||||
|
|
|
|
2221000 |
2211100 |
2111110 |
|
|
|
|
|
|
|
|
1111111 |
Fig. 1. The orbit partition. The
surface simplex (7,7) in 7-dimensional vector space. The distance between the neighbor
orbits is due to the exchange of 2 vectors only. The orbits are ordered into
columns according to the number of zero vectors, into the rows according to the
size of the longest vector. Such orbit diagrams can be formed by the full
induction for all m and n (it is the problem of the partition of the number m
into n parts). If m < n or n> m, the diagram is truncated, some orbits
can not be realized.
If we have the ideal gas system
(9) with its collisions, such a collision can be symmetrical, e.g. a5+
b2® a2+ b5. Two
vectors change their position and the system remains on the same orbit. But a
collision can be asymmetrical, e. g. a5+ b2® a3+ b4. The system changed
its orbit since the resulting partition is different.
As the result of a series of
asymmetrical collisions, the system can return on its initial orbit. If a
system has infinite many particles, collisions occur simultaneously, and the
system remains on an orbit or on a narrow band of orbits. Because the neighbor
particles meet at the collisions, we may suppose that the corresponding vectors
are indexed as neighbor, too, and we can imagine that the ideal gas system is
rotating in its equilibrium orbit. The state of the system is determined by the
symmetry of this orbit.
If we multiply n dimensional
vector row with natural coordinates (zero including) by the unit permutation
matrices P representing the group of cyclic permutations Sa, we
get
n!/Õ nk! /2/
Different points on an orbit
provided
S (k ³ 0) nk = n, S (k ³ 0) nkmk = m
/3/
Boltzmann proposed the logarithm
of this index (n-polynomial coefficient) as the entropy measure H.
B There was a
word at the beginning
The application of the H
function in the information theory is an example of sloppiness.
Shannon needed the name for the
function Hm = S pklog2 pk.
And J. von Neumann suggested him
entropy:”In the first place your uncertainty function has been used in
statistical mechanics under that name, so it already has a name. In the second
place and more important, no one knows what entropy really is, so in a debate
you will always have the advantage” (10).
But a more important objection
was that the probabilities in both applications were different. The ideal pas
system can be described by the linear vector. e.g. 3,2,1,1, 0 ... or a3,
b2, c1, d1, e0 .. The elements of
the vector are exponents corresponding to the energy which the particles have,
we need not know the positions of particles. But such a vector gives only the
statistics; it does not contain the information which is inside words. For
example, bacadaab and abdacaba are different words with the same statistics. In
the case of the ideal gas, it is the actual position of all particles which are
lost in the difference.
This information is exactly the
difference between a path in the space represented by a string of vectors and a
position in the space given by the vector sum.
At first we give a
straightforward interpretation of the information entropy with the binary
logarithm (11). In a message we have m symbols (
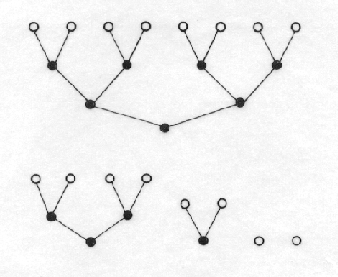
Fig. 2. Graph interpretation of
the information entropy. The entropy is given by the difference of the number
of edges in both coding graphs divided by the number vertices. If no
information about 8 objects is available, we need at least 24 decisions
(left-0, right-1) digits. If the objects are indexed as a, a, a, a, b, c, then
it is necessary only 8 such indexing steps. The difference divided by the
number of the objects, is the measure of information, which we have about the indexing.
But for information entropy
based on natural logarithms, we have another interpretation.
Words are vectors of information
and we interpret them as vector strings (12). For this purpose we identify the
symbol i with the unit vector ej and write a word in the form
of a vector column. The word has the form of the naive matrix. Which has in
each row one unit. Now we have two symmetry operations acting on a matrix Pm
NPn.
If we multiply a matrix by the
unit permutation matrix Pn from the right, we permute columns
of the matrix (it corresponds to substitutions of symbols). If we multiply a
matrix by the unit permutation matrix Pm from the left, we
permute the rows or symbols. In both cases the position vector remains on the
orbit.
Both symmetry operations are
separated, if we form the quadratic forms
PnNTNPn
and PmNNTPm.
Finding the quadratic form PnNTNPa
, we get from a text its statistics, we know only how many
symbols of each kind were in the text, but we do not know their order,
finding PmNNTPm , we know the pattern,
but we do not know which symbols were used. The formal mathematical operation
corresponds to the abstraction in thinking.
The statistics of N is known in
combinatorics as the distribution of m distinguishable things into n
distinguishable boxes and is determined by the sum of the products of two
polynomial coefficients (9).
S (n!/P
nk!) (m!/P mk!nk) = nm
/4/
The sum is made over all orbits
fulfilling /3/.
The statistics of PnNTNPn
is known as the distribution of m undistinguishable things into n
distinguishable boxes and it is given by the sum of the n polynomial
coefficients of all orbits
S (n!/P
nk!) = (m+n-1)!/m!(n-1)! /5/
Now we see the difference of
both entropies. The n-polynomial coefficient was used by Boltzmann; its
logarithmic measure gives Hn function. Similarly the m polynomial
coefficient gives Hm function which corresponds to the Shannon
entropy measure with the binary logarithm. In every case Hm is
different from Hn and can not replace Hn.
Thus all attempts to replace Boltzmann Hn function with entropies
derived from the theory of information (13, 14) were based on the incomplete
analysis.
The formalism of the symmetry of
the quadratic forms shows al so that the dispute about supposed
undistinguishability of microparticles was based on misunderstandings.
According to classical combinatorics, boxes (vectors) in NTN
are distinguishable and we can map each case onto the plane simplex and count
them. But according to the quantum physics, if a system can be permuted, its
particles should be undistinguishable. Actually they are only equivalent.
It could be argued that there is
difference between the polynomial coefficients and the equation /1/, but simple
calculations show how fast both results converge for small n and m.
C The mixing
entropy
Boltzmann and Shannon both used
the ergodic hypothesis; they supposed that their elements are good mixed. But
it is impossible using both measures H and H to measure the mixing entropy
which exists in physics.
If we have two binary strings
large enough
1 1 1
1 1 1 0 0 0 0 0 0 /a/
1 0 1
0 0 1 0 0 1 0 1 1 /b/
to form a book with two volumes,
then we can distinguish macroscopically /a/ and /b/ similarly as we distinguish
between two states of a system consisting from two compartments, one full of molecules
and the other empty in one state and mixed in another. But both strings lie in
m dimensional vector space on the same orbit which crosses the unit cube or
they lead to the same point in the 2-dimensional space (12), it is, all strings
have the identical entropy Hn and Hm.
We can interpret them in two
ways. Let us suppose that m is the volume of the system, the number of cells
which can be occupied by a molecule (then the value is 1) or can be empty (then
0). The indexing of the cells can be microscopically observable, it is /a/ is a
comprimed gas system, /b/ is the expanded system. Or 0 and 1 are just two kinds
of molecules and we follow their mixing. The entropy H is just the logarithmic
measure of the symmetry index given by the polynomial coefficient. This index
is the same for all parts on the orbit and it does not express the entropy of
mixing which should be connected with the position on the orbit.
This can be shown on a simple
example. Let us suppose that we have two isolated systems of the ideal gas A,
B, with the number of molecules and entropies HA and HB
and further that the system A is hotter than B and moreover, that both
distributions are ”iced”, there is none exchange of energy between particles.
The entropy of the system formed from two isolated systems is HA+B =
HA+ BB.
If we join both systems removing
the separating wall, the number of the particles in the system will be n = nA+
nB and its entropy
HAB = HA HB + ln n!/nA!(n-nA)!
This binomial coefficient is
just the number of all permutations of particles nA with particles nB
without regard on their energy, it corresponds to the changes due to the
diffusion, there are no collisions of particles. The term ln n!/nA!(n-nA)!
(seems to be the mixing entropy, we looked for, but it is not, because it only
characterizes the new orbit but not the position of the system on the orbit.
When we postulated the existence
of two subsystems A and B, we introduced into the n- dimensional vector
indexing. Because removing of the separating wall has no effect on the physical
space we can not change the indexing of the topological space and indexes in
both original parts must remain macroscopically distinguishable.
Boltzmann discussed effects of
collisions on the distribution of energy only and did not analyze the effect of
the position of particles on the equilibrium. He introduced the ergodic
hypothesis and neglected the possibility that the entropy can depend not only
on the partition, but on the ordering of vectors-particles on the partition
orbit. If the points of the partition orbits are not macroscopically
equivalent, then the Boltzmann formula does not include any term for the mixing
entropy.
Even the Shannon information
entropy H measures possibilities of m only. If the frequencies of the symbols
are constant, then the Hm value remains constant for all
permutations of symbols. If there are two physical processes affecting the
entropy, the exchange of energy between particles by their collisions and the
change of their positions due to the diffusion, we need also two different
mathematical measures isomorphic to both operations. Essentially there are two
possibilities. We can split the partition orbits into suborbits, as e.g. the
partition 1n corresponding to the group of cyclic permutations
S can be split into n subgroups according to their cyclic structure.
But it is doubtful if it gives
the right result. It gives too low estimates. By splitting the system into two
subsystems A and B, we introduced the binomial distribution. The orderings in
its string are measured by the negative binomial distribution which counts the
lengths of sequences of one kind. This distribution is the polynomial
distribution, which probability is measured by the polynomial coefficient. It
means that the mixing entropy is H again, only the measured values are not
values mk but distances between vectors of one kind.
Using cyclic indexing (n+1) = 1
we get for /a/ and /b/
111117
/a/
233211
/b/
We obtained again partitions and
we can use both measures Hn and Hm once more.
For usual texts the problem is
somewhat more complicated, we have many symbols and instead of the binomial
distribution we deal with the polynomial distribution. But the problem can be
simplified, the polynomial distribution is a set of the binomial distributions.
For example the string
abcdabaa
can be written as
a 0 0
0 a 0 a a
0 b 0
0 0 b 0 0
0 0 c
0 0 0 0 0
We can now calculate four
negative binomial distributions. Or alternatively, we can use directly the
naive matrix N which is the binary vector in mn-dimensional space and
apply to it the negative binomial distribution.
Using this method for physical
word or world, the mixing entropy measures distances between molecules of the
same kind; or having the same energy, how they are distributed inside their
matrix.
D. Symmetry of molecules and
information indices.
Till now we worked only with
symbols or with ideal molecules without any structures. But the reality is more
complicated. If we have n objects and m relations between them, we need to its
description the incidence matrix of a graph in which rows at least two unit
symbols must appear.
The entropic measures /1/ were
introduced on graphs by Rashewsky (15), Mowshowitz (16) and others. They are
known as topological information indices (17). They measure different graph
invariants. Using the naive matrices in (m+n) dimensional dual space, it was
possible to show that all them are different from the entropies as defined by
Boltzmann and Shannon.
The matrix
|
0 |
N |
|
NT |
0 |
is the adjacency matrix A
of a special kind of graphs -the star forests. At them the difference of Hn
and Hm and other topological information indices was obvious
(11).Topological information indices measure symmetries of graphs which are given
by the number of possible different configurations of a graph with labeled and
unlabeled vertices.
This symmetry was connected with
physical entropy of molecules by Gordon and Temple (18). We got the fourth set
of entropic measures H connected with entropy and we still do not know what the
entropy S really is.
D. The maximal entropy
Boltzmann found that the maximum
of H was achieved if the n energy distribution corresponded to the Maxwell
distribution. Then it was exponential and the distribution of velocities was
normal. The proof was based on the use of Lagrange coefficients.
But Shannon found the maximal Hm
straightforwardly. H is maximal if all Pk are equal. The
difference between the maximal Hm and the observed information
energy was called the redundancy. All observed information distributions have
rather high redundancy, they are not optimal for the
communication.
This fact is explained easily.
If all symbol s have the same frequency in the text, there exist the
maximal number of possible strings, obtainable by mere permutations. But the
given orbit contracted to 1 point and its H = D. If the frequencies of symbols
are different, then different combinations of symbols give more different
messages, Hm is maybe lower, but the sum Hn + Hm
is higher. The natural languages do not maximalize Hm but the sum of
entropies and this explains the observed redundancy easily.
If we think in terms of words
(molecules of information formed from its atoms-symbols), we distinguish easily
the theme it is spoken about if not all words occur uniformly. If we use
Shannon’s direct approach for Hm, we find that H should be maximal,
if each nk = 1. It means that the maximum of the function H is not
achieved at the Maxwell distribution but at the linear n distribution.
Boltzmann’s proof was based on a mathematical maneuver, but why the nature
accepts it?
The condition nk = 1
means that each particle should be in its own energy state which is possible
only if the total number of quanta is greater that the sum of the linear line
m
> n(n+1)/2.
The mean energy m of 1 particle
should be then greater then the half of the number of particles in the system
mj³ (n+1)/2
Comparing the Boltzmann constant
k in the form k= 2,O8.1O1O h/grad, where h is the Planck
constant, with the Avogadro number N=6,023.1023, we see that the
linear distribution could be achieved in the normal range of temperatures only
for very small systems with the number of particles less than 10-13
mols or for molar size systems at temperatures higher than 1013 K.
Supposing that no other entropy were effective.
E
Perspectives
The elementary analysis of
mathematical entropy measures H showed that they can be explained consistently
on an elementary level. They are connected with the notion of symmetry. Its
elements seem to be trivial, but complications are towering fastly in wreath
products. It is a long way from a string of symbols to superstrings which
appear in contemporary physics. The physical phase space is not as plain as the
ideal Euclidean space is and it will be long before we decipher all letters of
the alphabet of a strange language the Nature is written in.
Literature Cited
1. Peres A., Phys. Rev. Lett. 1985, 63,
1114.
2. Weinberg
S., Phys. Rev. Lett. 1989,
63, 1115.
3. Bowen L.H., J. Chem. Educ.
1988, 65, 50.
4. Pojman, J., J. Chem. Educ.
1990, 67, 200.
5. Clugston M.J., J. Chem. Educ.
1990, 67, 203.
6. Swanson R. M., J. Chem. Educ.
1990, 67, 206.
7. Boltzmann
L., Wien. Ber. 1877, /6, 373.
8. Shannon C.,
Bell System Techn. J. 1948,
27, 623.
9. Kunz M., Physics Letters A
1989, 135, 421.
10. Shaw O., Davis C. H. J. Am.
Soc. lnform. Sc.1983, 34, 67.
11. Kunz M., Coll. Czech. Chem.
Commun. 1986, 51, 1856.
12. Kunz M., lnformation
Processing and Management, 1984, 20, 519.
13. Jaynes E.T., Phys. Rev.
1954, 106, 620.
14. Brillouin L., Science and
lnformation Theory, Academic Press, New York, 1956.
15. Rashewsky N., Bull. Math.
Biophys. 1955, 17, 229.
16. Mowshowitz A., Bull. Math.
Biophys. 1968, 30, 175, 225, 387, 533.
17. Balaban
A.T., Motoc I., Bonchev O., Mekenyan O., Topics Curr. Chem. 1983, 114, 21.
18. Gordon M., Temple W.B., J.
Chem. Soc. 1970, 729.