|
|
|
WWW: Enigma její statistiky
Milan Kunz
Dva nejprestižnější světové vědecké časopisy Nature (1) a Science (2) přinesly statistiku spojitosti Internetu, kterou zjistili Albert a Barabasi (maďarsky znějící jména, ale jsou to fyzici pracující v USA). 325726 míst Internetu má průměrný počet připojení 5,46. Připojení jsou rozdělena velmi nerovnoměrně. Na každých 100000
míst s jen jedním připojením připadne jen asi 1000 míst s deseti připojeními a jen asi 10 míst se sto připojeními.Tato statistika ukazuje nevhodnost přirovnání Internetu k mozku. Vzhledem k prostorovým omezením se mohou jednotlivé mozkové buňky spojovat nervovými vlákny, axony, pouze k několika dalším neuronům. Velká centra WWW bychom měli srovnávat s celými oblastmi mozku, jako je třeba centrum řeči. I když je WWW nový jev, samotná statistika vůbec nepřekvapuje, protože má stejný tvar, jako všechna známá
rozdělení informace. Co překvapuje, je to, že v oněch renomovaných časopisech nikdo nežádal, aby autoři doplnili do svých článků příslušnou literaturu. Tak to musíme udělat za ně.Kdybyste si dali práci a spočítali frekvenci písmen třeba v tomto článku, zjistili byste, že některá se vyskytují velmi často (a, e, o, p) a jiná velmi zřídka (x, q, ů, ó)
Když Shannon formuloval svou teorii komunikace (3), považoval tento fakt za škodlivý pro ekonomiku spojení, protože z hlediska přenosu zpráv by bylo optimální, kdyby všechny symboly ve zprávě byly využity rovnoměrně. Nazval tento jev nadbytečností (redundancí).
Fysik Brillouin, kterému prý unikla Nobelova cena za fysiku, rozvinul kolem tohoto faktu řadu spekulací (4). Považoval informační entropii za jakýsi protiklad fyzikální entropie a říkal ji negentropie. S růstem informace by měla klesat entropie a naopak.
Už před padesáti léty se nadbytečnost lidské řeči pokoušel pragmaticky využit pan Zipf. Chtěl určit, jaká slovíčka se mají přistěhovalci naučit jako prvá, aby se v nové zemi, USA, co nejrychleji dorozuměli. Výsledkem jeho práce byla pořádková statistika. Nejčastěji se vyskytující slovo (v angličtině určitý člen the) se vyskytovalo několikrát častěji (nebo jinak, tvořilo několikrát větší podíl textů) než slov
o druhé. Frekvence slov v logaritmické stupnici krásně korelovala s jejich pořadím ve frekvenčním slovníku. Dá se předpokládat, že pořádková statistika by se mohla aplikovat i pro Internet.Příčina nadbytečnosti lidské řeči se dá vysvětlit docela jednoduše podle rčení: Já o koze, on o voze. Kdyby se všechny hlásky vyskytovaly stejně často, dalo by to moc práce, jednotlivá slova rozlišovat. Obvykle se snídají jiné pokrmy než ty, které se jí k večeři. Slova (kromě pomocných slov) se přitom využívají podle potřeby. Co je optimální z hlediska komunikace, není zrovna nejlepší pro informaci. Podle frekvence hlásek se dá rozeznat použitá řeč, podle frekvence slov se dá rozeznat o čem ta řeč je.
Téměř současně se Zipfem si americký statistik Lotka dal práci se spočítáním počtu publikací jednotlivých autorů v desetiletém rejstříku Chemical Abstracts (5). Neznám podnět k jeho práci. Za druhé světové války za německých náletů na Anglii se utěšoval jiný statistik, Yule, tím, že zjišťoval frekvenci podstatných slov ve svý
ch zamilovaných knihách.Oba statistici použili metodu jako Albert a Barabasi a dospěli už tenkrát ke stejnému výsledku. Nejčastěji se objevili autoři s jednou publikací nebo slova použitá jen jednou. Autoři s jednou publikací tvoří vědecký plebs, jsou asi málo schopní nebo líní chudáci, kteří se nezmohli na víc, nebo jsou to pouzí pomocníci připsaní některým koryfejem vědy z milosti na společnou publikaci. To zvláštní slovo (koryfej, neměl bych jej opakovat, už se dostalo do skupiny slov použitých dvakrát
a ztratilo svůj glanc) jsou slova řídká a proto vzácná. Pečlivým autorům dá hodně práce, aby je vyhledali ve své paměti nebo v nějakém jiném thesauru. Jejich vysoký podíl v textu se považuje za příznak dobrého stylu.Dodnes bylo shromážděno desetitisíce podobných statistik. Všechny údaje mají podobný základní tvar extrémně kosého rozdělení. Snad největší sbírku takových příkladů měl inženýr Vlachý.
Ruský učenec Haitun považoval tento tvar rozdělení za specifický pro informaci (6), ačkoliv ve Vesmíru je základní (počty částic od vesmírného prachu přes hvězdy k černým dírám).
Počátky statistiky korelují většinou dobře, čím jsou soubory větší, tím lépe, ale konce statistik (ohony) jsou rozptýlené, mlhavé. Tady se nejvíce projevují náhodné vlivy.
Podobný tvar má
i Zipfova statistika, kde se těžko zachycují skutečné frekvence vzácných slov. Při tom se většinou dají oba typy statistik, pořádková i frekvenční, použít pro stejné údaje.Řada matematiků našla příslušné vzorce pro obě statistiky. Co je však velmi podivuhodné, je existence vnitřní korelace. Když se vynesou na jednu osu třeba počty autorů s x publikacemi proti počtu publikací y x-tého autora, dostane se v dvojité logaritmické přímka (7, obr.1). To jistě platí i pro statistiku Internetu.
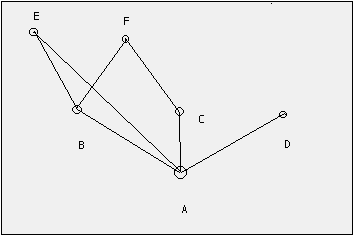
Obrázek 1: Korelace hlava-ohon Podle Lotkových údajů. Začíná u r = 2, údaje pro r = 1 leží mimo přímku.
Zipfova a Lotkova statistika nejsou jedinými možnými způsoby pro korelaci podobných dat. Nositel Nobelovy ceny za fyziku Shockley použil pro vyhodnocení svých podřízených počtu jejich publikací jednoduše papír s logaritmicko normálním rozdělením (8). Rozdělení logaritmicko normální je useknuté frekvencí 1, jejíž logaritmus je 0. Při tom podíl objektů s touto frekvencí je blí
zký polovině všech objektů. Obvyklé algoritmy pro výpočet hodnot logaritmicko normálního rozdělení proto selhávají.Při použití logaritmicko normálního rozdělení je obvykle podíl objektů s nejnižšími frekvencemi vyšší, než by odpovídalo ideálnímu rozdělení.
To se dá napravit exotickou substitucí z = log2(x + 1)!, která dá pro x = 1 log z = 0 (9).Tak jsme se dostali k rovnicím a bude potřeba několik vysvětlení.
Trochu matematiky
Internet se liší od jednoduché řady slov v textu (rejstřík Chemical Abstract je text, ve kterém jsou jednotlivé publikace (lze považovat za opakování symbolu představovaného celým jménem autora) shrnuty na jedno místo, tím že se jedná o síť. Avšak i autoři vytvářejí síť. Protože existuje instituce spoluautorství, vytváří se sítě auto
rů. Maďaři by mohli vědět o existenci Ramsayova čísla, jak daleko je někdo v grafu spoluautorů od Erdose. Použijeme také teorii grafů, jako Albert a Barabasi.Nejdříve zdánlivě jednoduché věci proměníme ve složitý problém. Řadu slov v textu si znázorníme pomocí matice, kterou jsem nazval naivní (10). Místo symbolů budeme psát jen jednotky do sloupců jejichž číselný index j odpovídá pořadí daného symbolu v abecedě (jinými slovy, indexování je lexikografické. Pro pořadí symbolu v textu budeme používat řádkový
index i. Slovu abcba bude odpovídat zápis 111122133142151 nebo 11a12b13c14b15a, což ukazuje, že v textu je index i vlastně nadbytečný. Názorněji se zapíše abcba jako matice N s třemi sloupci a pěti řádky:|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
S maticí N
můžeme provádět operaci zvanou permutace, při které měníme pořadí sloupců (n permutace) nebo řádků (m permutace).N permutace změní slovo abcba třeba na acbca, m permutace změní slovo abcba třeba na aabbc, což se může považovat za základní tvar.
K
popisu Internetu musíme použít složitější matice S, které se říká incidenční. Prvky matice S jsou sij = -1, pokud i-tá orientovaná hrana (spojení) vychází z vrcholu j, sij = 1, pokud i-tá orientovaná hrana končí ve vrcholu j, jinak sij = 0.Když přepíšeme
|
1 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
-1 |
0 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
–1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
0 |
-1 |
0 |
0 |
|
0 |
1 |
0 |
0 |
0 |
0 |
-1 |
0 |
|
1 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 |
dostaneme incidenční matici
S hvězdného lesu. Vrchol a má dvě hrany, vrchol b má také dvě hrany a vrchol c má jednu hranu, každá hrana má svůj vlastní index. Názvosloví teorie grafů je poetické. Grafům bez cyklů říká lesy, vrcholům lesů s jenom jednou hranou listy, množině stromů les.Graf Internetu se liší od grafu lesů tím, že se v něm vyskytují cykly, což znamená, že vrchol a je spojen s vrcholem b, vrchol b je spojen s vrcholem c, a tak dále, až vrchol x je spojen s vrcholem a.
K incidenční matici
S můžeme najít její kvadratické formy STS a SST. Nás bude zajímat matice STS, známá jako matice Laplace-Kirchhoffa. Laplace použil matice tohoto typu jako prvý a Kirchhoff je použil k popisu elektrických sítí.Internet není vlastně nic jiného než elektrická síť, ve které se informace pohybují ve formě elektronů.
Laplace-Kirchhoffovu matici můžeme formálně rozdělit na
diagonální matici V, jejímiž prvky jsou počty hran (Albert a Barabasi zjistili tuto matici) a matici mimodiagonálních prvků A, STS = V - A. Matice A je známá jako matice sousedství (adjacency). Albert a Barabasi se zabývali maticí V.Teď bychom se mohli věnovat teorii Laplace-Kirchhoffových matic (11). Spokojíme se s jejím rozdělením na dvě matice. Albert a Barabasi se zabývali maticí
V. Tuto matici dostaneme také jako kvadratickou formu matice N. NTN je matice N násobená transponovanou maticí NT zleva. Je to jen diagonální matice V, matice mimodiagonálních prvků A je v NTN nulová. Nebo můžeme rozsekat síť na hvězdný les, graf všech center se všemi linky spojenými s těmito centry (každé spojení se bude počítat dvakrát).Když se budeme zabývat počtem možných lesů (12), zjistíme, že závisí na dvou polynomických koeficientech, jeden odpovídá permutaci sloupců (n permutace), druhý odpovídá permutaci řádků (m permutace). Tím se dostáváme k dalšímu klíčovému problému, k informační entropii a fyzikální entropii
a jak se skutečně projevují.Informační a fyzikální entropie
Abychom oddělili vliv n a m permutací, budeme se zabývat nejprve kvadratickou formou matice
N, NTN. To jsou pro náš příklad čísla 2,2,1. Existují tři možnosti změny jejich pořadí: (2,2,1), (2,1,2) a (1,2,2). Tomu odpovídají řady aabbc, aabcc a abbcc. Počet n permutací se zjistí pomocí polynomického koeficientu, který má tvarn!/P nk!
kde n! znamená n faktoriálně (n! = 1*2*3*4*...*n), n je počet sloupců matice, P
je symbol pro násobení a nk je počet sloupců matice se stejným počtem k jednotkových prvků ve sloupci matice, nebo počet stejných prvků diagonální matice NTN. Funkce faktoriálu má jednu podivuhodnou vlastnost, že 0! = 1. To znamená, že pokud nk je nulové, hodnota polynomického koeficientu se nemění a k může být v intervalu nula - nekonečno. Každý index k se vyskytuje pouze jednou, avšak hodnoty nk pro různá k mohou být stejné.Vezmeme-li základní řadu aabbc, počet m permutací (permutace pořadí symbolů) je 15, což je výsledek pro 5!/2!2!1!. K tomuto výsledku se dostaneme použitím polynomického koeficientu, který má tvar
m!/P mj!
kde m je počet řádků matice (počet symbolů), m
j počet výskytu (frekvence) symbolu j. Protože v textu se mohou vyskytovat symboly se stejnou frekvencí, jejich počet jsme výše označili jako nk, je možné vzorec přepsat tím, že sdružíme hodnoty mj se stejnou frekvencí k .Po logaritmování mají oba polynomické koeficienty tvar
log n! -
log m! -
S nklog mk! (2).Oba polynomické koeficienty se při výpočtu počtu všech matic (řad) násobí a tedy jejich logaritmy se sčítají. Teď se dostaneme k počtu možných hvězdných lesů a tím sítí a Internetů.
Místo logaritmy tohoto polynomického koeficientu lze použít jinou názornější funkci, a to počty hran binárního rozhodovacího stromu s kořenem (obr 2).
Jako dříve bude abstraktní symbol (či jiný vektor informace) představovat kořen a jeho jednotlivé výskyty v seznamu jeho listy, kterých je vždy mj. U binárního rozhodovacího stromu s kořenem budou listy spojeny s kořenem větvemi, odpovídajícími číslicím 0 (vlevo) a 1 (vpravo). Listy tak budou indexovány řadou nul a jednotek, která se liší od obyčejného binárního čísla tím, že obsahuje nadbytečné 0.
Pro takové indexování m objektů budeme potřebovat minimálně mlog2m symbolů. Pokud je těchto m objektů rozděleno do n podmnožin, pak se počet symbolů potřebných pro jednoznačné indexování sníží. Rozdíl (viz rovnici 2) můžeme považovat za míru informace, kterou o dané množině máme (12).
Kdyby se jejich počet určoval jen podle n permutací, potom by bylo nejlepší kdyby polynomický koeficient pro n permutace měl tvar n!/1!*1!*1!...1n!. To znamená, že každý vrchol by měl jinou frekvenci. Takový počet hran má úplný graf (každý vrchol je spojen se všemi ostatními). Průměrný počet př
ipojení v takové síti je však mnohem vyšší než počet vrcholů sítě, což jistě není případ Internetu, kde průměrný počet připojení je relativně malý (5,46).
Obrázek 2. Jednoznačné určení osmi prvků pomocí binárního rozhodovacího stromu. Potřebujeme 24 symbolů. Pokud jsou prvky označeny (aaaabbcd), potřebujeme jen 14 symbolů. Rozdíl po dělení počtem prvků dá H = 1,75, v tomto zjednodušeném příkladě přesný výsledek.
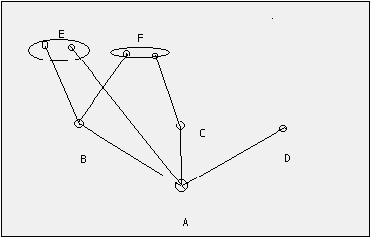
Našli jsme elementární speciální řešení. Aplikace metody vyšší matematiky vedla k jinému řešení, že optimální je exponenciální rozdělení.
A kdyby se počet hvězdných lesů určoval jen podle m permutací, potom by bylo nejlepší kdyby polynomický koeficient pro m permutace měl tvar m!/1!*1!*1!...1n!. To je splnitelné pro m = n, počet připojení by měl být stejný jako počet vrcholů a průměr by byl 1. Optimum pro jiné poměry m ku n je vždy průměrná hodnota m/n. Jenže potom n
k = n, všechna mj či mk jsou stejná a polynomický koeficient pro n permutace má minimální vždy hodnotu 1.Oba polynomické koeficienty vytváří různé tendence, pokud se mají optimalizovat. Polynomický koeficient pro n permutace vede k rozmanitosti, polynomický koeficient pro m permutace vede k nivelizaci.
Polynomický koeficient pro n permutace
spojil Boltzmann (13) s termodynamickou entropií, když vyslovil domněnku, že tato entropie je úměrná logaritmu tohoto koeficientu, nebo jinak logaritmu pravděpodobnosti (počet stavů ke všem stavům). To vedlo k rovniciS = -kS (nk/n)log(nk/n).
Shannon (3)
použil pro informační entropii rovniciH = -kS nk(mk/m)log(mk/m).
Pokud jsou současně možné oba typy permutací, potom se oba polynomické koeficienty násobí, což znamená, že jejich logaritmy se sčítají. Třeba soustava molekul ideálního plynu, které si předs
tavujeme jako pouhé body, jsou reprezentovány jen maticí NTN. Zde nemají smysl permutace jednotlivých kvant energie, vytvářené rychlostí pohybu molekul v soustavě. U molekul reálného plynu m permutace mohou být závislé na tvaru molekul, rozdělení hmotností a podobně.Nalezení optima současně pro oba polynomické koeficienty je velmi obtížné, zvláště pokud se optimum má hledat pro hodnoty m a n relativně malé ve srovnání s Avogadrovým číslem N nebo Boltzmannovou konstantou k, takže použití metod analýzy je problematické (třeba aproximace faktoriálu pomocí Stirlingova vzorce). Lze vyslovit jen tvrzení, že Internet asi není nejdokonalejší, ale je asi nejpravděpodobnější ze všech možných.
Nebo jinak lze říci, že má nejvíce prvků symetrie. Při tom si musíme uvědomit, že dokonalá symetrie znamená existenci pouze jediného prvku symetrie, identity. Větší počet prvků symetrie znamená větší počet možných uspořádání a tedy větší flexibilitu.
Shannon navrhl měřit informaci na logaritmické stupnici. Jestli je množství informace úměrné logaritmu frekvence, potom je rozdělení informace Internetu vlastně normální a není co vysvětlovat.
Rozdělení informace vznikají různými mechanismy. Rozdělení slov vytváří jednotlivec zcela mimovolně, když se snaží vyjádřit své myšlenky, jiná rozdělení vznikají zdánlivě nekoordinovanou činností nezávislých jednotlivců.
Sola Price, který se zabýval problémy rozvoje vědy, zastával optimistickou teorii, že úspěch budí úspěch. Prvé publikace usnadňují vytvoření dalších, prvé použití slova vytváří tendenci, abychom je opakovali. Ke stejnému výsledku však vede pesimistický algoritmus vysvětlující rozdělení bohatství (Paretův zákon, platící pro rozdělení majetku a když považujeme vědomosti za majetek, potom Zipfův a Lotkův zákon jsou jen zvláštní příp
ady Paretova zákona). Podle Bible prý tomu, kdo má, bude přidáno, a tomu, kdo nemá, bude vzato i to, co má.Když se pro oba modely vytvoří urnový model, příslušné algoritmy (14) vedou ke stejnému výsledku.
Literatura a poznámky
1. R. Albert, H. Jeong, A-L. Barabasi, Nature, 401, 130 (1999).
2. A-L. Barabasi, R. Albert, Science, 286, 509-512 (1999).
3. C. E. Shannon, Bell System Techn.,J., 27, 379, 623 (1948).
4. L. Brillouin, Science and Information Theory, Academic Press, New York, 1956.
5. Viz například
Czech. J. Phys. B36, No. 1, který editoval J. Vlachý, věnovaný šedesátému výročí Lotkova zákonu, a sérii příspěvků J. Vlachého v tomto časopise.6. S.D. Haitun, Scientometrics, 4, 5-25, 89-10, 5, 375-395. (1982), M. Kunz, Scientometrics, 13, 289-297 (1988).
7. M. Kunz, Scientometrics, 13, 289-297 (1988).
8. W. Shockley, Proceedings IRE, 45, 379 (1957).
9. M. Kunz, Scientometrics, 18, 179-191 (1990).
10. M. Kunz, J. Chem. Inform. Comput. Sci., 33, 193-196 (1993).
11. M. Kunz, J. Math. Chem., 9, 297-305 (1992).
12. M. Kunz, Coll. Czech. Chem. Commun., 51, 1856-1863 (1986).
13 L. Boltzmann, Wiener Berichte 76, 373 (1877).
14. M. Kunz, Scientometrics, 11, 163-173 (1987).