|
|
|
About Eigenvalues of the Normalized Graph Matrices
Milan KUNZ
Jurkovičova 13, 63800 Brno, The Czech Republic
2. November 2002
e-mail: kunzmilan@seznam.cz
Abstract
The eigenvalues of normalized Laplace-Kirchhoff matrices of trees STV-1S and V-1/2SSTV-1/2 are compared with the eigenvalues of original Laplace-Kirchhoff matrices. Some properties of the normalized graph matrices are discussed.
Introduction
I have shown that the off-diagonal elements of normalized Laplace-Kirchhoff matrices STV-1S are a source of the Randic index, and the sum of their inverses then forms the normalized Wiener index [1-5].
Recall that the incidence matrix S has elements sij = -1, when the arc i goes from the vertex j, sij = 1, when the arc i goes to the vertex j, sij = 0, otherwise.
The incidence matrix S has two quadratic forms, one known as the Laplace-Kirchhoff matrix STS, and the other form is SST.
The matrix STS can be decomposed into the diagonal matrix V of vertex degrees vii and the off-diagonal matrix A, known as the adjacency matrix (aij = 1, if the vertex i is incident with the vertex j, aij = 0 otherwise).
The eigenvalues of the normalized scalar product of the incidence matrix S are identical with the eigenvalues of the other normalized scalar product of the incidence matrix
V-1/2SSTV-1/2, except the zero eigenvalue. This eigenvalue is missing at V-1/2SSTV-1/2 of trees since these sqare matrices have only (n-1) rows and columns. It is interesting to study how the normalization changes the eigenvalues normalized matrices.
RESULTS
For evaluating the effects of the normalization, the set of heptanes is suitable, since it shows different structures. The zero eigenvalue is omited from the following table.
U - unnormalized eigenvalues
N - normalized eigenvalues
Heptane | Eigenvalues | ||||||
n-heptane | U | 3.8019 | 3.2470 | 2.4450 | 1.5550 | 0.7530 | 0.1981 |
N | 2 | 1.8660 | 1.5 | 1 | 0.5 | 0.1340 | |
2-Me-hexane | U | 4.2283 | 3.3604 | 2.1859 | 1 | 1 | 0.2254 |
N | 2 | 1.8466 | 1.3408 | 1 | 0.6591 | 0.1531 | |
3-Me-hexane | U | 4.3342 | 3.0996 | 2.2742 | 1.4055 | 0.6262 | 0.2603 |
N | 2 | 1.8164 | 1.5 | 1 | 0.5 | 0.1835 | |
3-Et-pentane | U | 4.4142 | 2.6180 | 2.6180 | 1.5858 | 0.3820 | 0.3820 |
N | 2 | 1.7071 | 1.7071 | 1 | 0.2929 | 0.2929 | |
2,4-diMe-pentane | U | 4.4142 | 3.7321 | 1.5858 | 1 | 1 | 0.2679 |
N | 2 | 1.8157 | 1 | 1 | 1 | 0. 1834 | |
2,3-diMe-pentane | U | 4.6287 | 3.2297 | 2.1397 | 1 | 0.6802 | 0.3217 |
N | 2 | 1.7671 | 1.4339 | 1 | 0.5656 | 0.2324 | |
2,2-diMe-pentane | U | 5.0965 | 3.1169 | 1.4911 | 1 | 1 | 0.2955 |
N | 2 | 1.7905 | 1 | 1 | 1 | 0.2094 | |
3,3-diMe-pentane | U | 5.1642 | 2.6180 | 2.2271 | 1 | 0.6086 | 0.3820 |
N | 2 | 1.7071 | 1.5 | 1 | 0.5 | 0.2626 | |
2,2,3-triMe-butane | U | 5.2618 | 3.3399 | 1 | 1 | 1 | 0.3983 |
N | 2 | 1.7067 | 1 | 1 | 1 | 0.2928 | |
The normalized Laplace-Kirchhoff matrices have the largest eigenvalue equal to 2, and the fourth largest eigenvalue is 1. The plots between original and normalized eigenvalues are more or less parabolical. The eigenvalues show some rounding errors, their sums should be always 2(n-1) or n, respectvely. The normalized eigenvalues are more complementary, , they appear as pairs, e.g. 2,2,3-triMe-butane normalized eigenvalues are paired as (2, 0), (1.7067, 0.2928), (1, 1), (1).
The eigenvector of the largest eigenvalue 2 is the unit vector row (column) J (JT) which sums the normalized elements. Each arc of the graph of neibourhoud SST coincides with (vi + vj) neighbour arcs. At normalization, these elements are divided by vi or by vj, respectively, by separate operations V-1/2S and STV-1/2. The final product gives in each row vi elements 1/vi and vj elements 1/vj. Their sum in each row (column) is just 2.
The normalized matrices V-1/2SSTV-1/2 of stars Sn have elements sii =n/(n-1), sij = 1/(n-1) (supposing that all arcs go from the root). Thus, their eigenvalues are 2, 1n-2, 0. The inverse matrices (V-1/2SSTV-1/2)-1 have elements sii =(2n-3)/(2n-2), sij = -1/ (2n-2). The sum of these normalized matrices gives the normalized Wiener index as Wn = (2n-3)/2.
A rather interesting effect of normalization appears at linear chains. Recal, that the eigenvalues of the adjacency matrices A form the cosine function 2cos(k 2
π/[n+1]), and matrices STS and SST have eigenvalues of the matrices (2I + A) with (n - 1) rows and columns, where I is is the unit diagonal vector. Again the cosine function appears, but now in the form 2cos([k-1]2π/[n-1]), This effect of normalization can be shown of the n-pentane (n = 5).Matrix | Factor | Eigenvalues | ||||
A | 2x | 0.866 | 0.5 | 0 | -0.5 | -.866 |
Degrees | 30 | 60 | 90 | 120 | 150 | |
A norm | 1x | 1 | 0.707 | 0 | -0.707 | -1 |
Degrees | 0 | 45 | 90 | 135 | 180 | |
The normalization spans the interval of the cosine function to the whole 2
π.The trace of the inverse of the quadratic form SST of acyclic graphs gives the Wiener number W. The elements of these inverses are walks exploited by corresponding arcs. The normalized inverses of the quadratic form V-1/2SSTV-1/2 are defined simply as combinatorial numbers. For example, we show (V-1/2SSTV-1/2)-1 of the linear chain L5. For simplicity, its 8 multiple:
7 | 5 | 3 | 1 |
5 | 15 | 9 | 3 |
3 | 9 | 15 | 5 |
1 | 3 | 5 | 7 |
The matrix is symmetrical. The elements on the diagonal and above it are the products [2(n - j) -1](2i - 1)/2(n - 1), The normalized Wiener number Wn is the sum of the diagonal elements of this inverse, or the sum of the inversed eigenvalues:
W(n) = S(2k �"1)(2n +2k �"1) /2(n-1)
where k goes from 1 till n �"1.
The properties of inverses allow to define the reccurent formula for the sums
w(n) = S(2k �"1)(2n +2k �"1)
as differences of the adjacent diagonals
w(n+1) = 2w(n) �" w(n-1) + 4n �" 8.
The recurrent formula for the normalized Wiener index Wn is thus
Wn = 2Wn-1 + Wn-2 + 4(n - 1).
The relation between the normalized Wiener index Wn and the normal Wiener index W of the linear chains can be inspected in the following table
n | W | Wn |
2 | 1 | 0.5 |
3 | 4 | 1.5 |
4 | 10 | 3.166 |
5 | 20 | 5.5 |
6 | 35 | 8.5 |
7 | 56 | 12.166 |
8 | 84 | 16.5 |
9 | 120 | 21.25 |
The relation between both indices is
Wn = 0.5084W0.7918
with r =1.000 and the standard deviation s = 0.3219.
The relation of both types of the Wiener number at heptane isomers is almost linear
Heptane | W | Wn |
n-heptane | 56 | 12.1867 |
2-Me-hexane | 52 | 10.8352 |
3-Me-hexane | 50 | 10.1684 |
3-Et-pentane | 48 | 9.5001 |
2,4-diMe-pentane | 48 | 9.5034 |
2,3-diMe-pentane | 46 | 8.8355 |
2,2-diMe-pentane | 46 | 8.8332 |
3,3-diMe-pentane | 44 | 8.167 |
2,2,3-triMe-butane | 42 | 7.5011 |
The relation is
Wn = 0.3344W - 6.5496
r = 1, standard deviation = 0.00456.
At stars, W = (n - 1)2. The relation is
Wn = 1.458W0.4099
r = 1, standard deviation = 0.00456.
Discussion
The normalized Wiener number Wn of stars grows more slowly that he normalized Wiener number Wn of linear chains. Both correlations with n are exponential. The surface between both courves forms the space, where alkanes can be found, see the following raw drawing
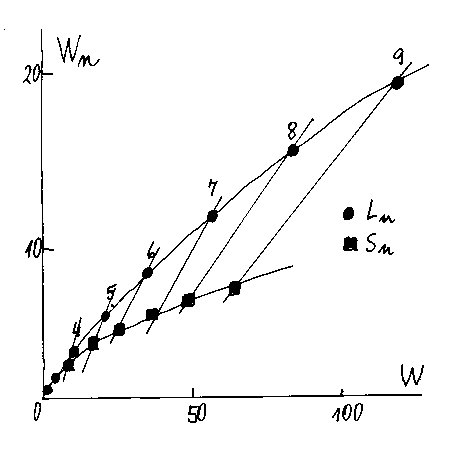
This kind of relation of physical properties with the Wiener index was observed at some physical properties of alkanes, as in [6]. Thus, the normalization could improve these correlations and explain their form.
References
[1] M.Randic, J.Math.Chem., 7{1991}155.
[2] M.Kunz, Collect.Czech.Chem.Commun., 54{1989}2148.
[3] H.Wiener, J.Amer.Chem.Soc., 69 {1947}17.
[4] M.Kunz, J.Math.Chem.,
[5] M.Kunz, Coll.Czech.Chem.Commun., 55{1990}630.
[6] I. Gutman, T. Kortvelyesi, Z. Naturforsch. 50a{1995}669