Jurkovičova 13, 63800 Brno, The Czech Republic

Statistical calculations are now easy due to computers and commercial programs. Therefore, we must be careful with data, we put in. For example, can zero counts be omitted as at Lotka visual analysis(1)? Is a rate of papers publishing or citing a value corresponding to physical velocity (first moment) or energy (2) (second moment) of the author (the cited paper), respectively? Distances in metric space (3), should be measured as straight ones (Euclidean), or as squared ones (Hilbert)?

Scientometricians are using direct counts. It seems obvious, that such counts are first metrical moments. A similar situation existed in the field of chemical applications of the graph theory. Distances in graphs were determined as numbers of edges on a path between two vertices. The sum of distances between all pairs of vertices is known as the Wiener number W, which correlates well with many physical properties of compounds. The distances between vertices ij are arranged into distance matrices D. Geometrical analogs of such distance matrices D were calculated (4), in which straight distances between atoms in molecules were inserted. I objected (5), but I was not able to show the right answer till I was emotionally excited (my note in an essay about the Schroedinger cat (6), that we do not understand mathematics properly, was reprimanded by experts (7). Exploiting the second moments of distance (6), squared Euclidean (Hilbert) distances, gave distance matrices having properties (the number of eigenvalues, angles between vertices) corresponding to the symmetry of the graph configuration.

Due to the importance of the citation analysis, its theoretical background should be improved, too. A practical question at evaluation of citation impact is, if indirect citations, citing papers which cited the parent paper, or mentioning names only, without references, need to be counted in comparison of two parent papers and which weight they should have. The answer, I propose, is based on mathematical arguments.

For example, let us have a citation pattern as on Fig. 1,

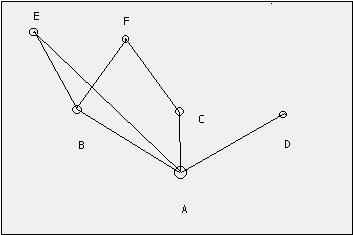
where A is cited by B, C, D and E directly and by E and F indirectly through B and C, when F is citing both B and C. This citation pattern generates a citation tree on Fig. 2,

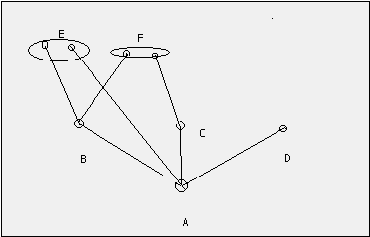
 where citation are torn out from citing papers as separate information vectors.

Citation trees are rooted trees, having the parent paper as the root. Different rooted trees are mapped onto n dimensional Euclidean space by numerical code (7). Such a code can be in the form of coordinate matrices C, which elements c(ij) = 1, if the citation i is on the same branch with the antecedent reference j, and c(ij) = 0 otherwise. Matrices C are in the lower triangular form and have unit elements in the first column and on the diagonal. The definition allows existence of rooted forests, if the paper j is not citing any from previous references and forms a new root (then in the first column zero appears, replacing the unit element).

Examples of rooted trees with three descending citations are given on Fig. 3.

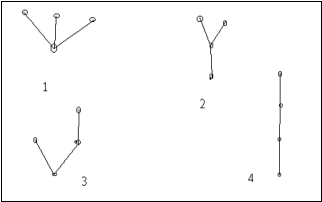
Corresponding matrices C are

If we omit column 1 as a dummy, it is easy to place 4 points of all configurations on the cube.

Matrices C are nonsingular and they have inverse matrices with the property CC^-1 = I.

The inverse matrices C-1 are

Notice, that the negative subdiagonal elements of these inverses C^-1 count in all columns only children, the number of all descendants is given as the total sum of all columns. It is possible to write matrix C^-1 as the sum of two matrices, the unit diagonal matrix I and matrix Dc, C^-1 = (I + Dc). Similarly, matrix C is a sum of two matrices, the unit column J and the block matrix formed from the zero column O and matrix D, which unit elements count vertices on each path from the root, or give coordinates of the vertex i. The number of unit elements is the distance of vertex i from the root, C = (J + OD).

Returning to Fig. 2, there were the counts of children in columns of the matrix Dc: 4, 2, 1, 0, 0, 0, respectively. This gives the number of all descendants.

Even if the count of all descendants is formally justified, it is desirable to have a more subtle measure for evaluation of citation trees. Intuitively, to be cited directly is better than indirectly. Therefore, tree A is the best and tree D is the worst, trees B and C lie between these two limits.

The measure could be simply the inverse of the number W of elements of corresponding matrices D, counting distances from the root: 1/3, 1/4, 1/5 and 1/6, respectively.

If it seems to be simple, then lets to be the measure the inverse of the sum of the singular values of matrices D, which is equal to the trace of the quadratic forms DD^T or D^TD, where M^T is the transposed matrix M. This reminds, that simple counts are simultaneously squared Euclidean distances since we did not find their square roots.

Using the inverse of distances as a measure is sufficient, if citation trees with an equal number of citations are compared. For comparison of citation trees with different number of references, this measure must be multiplied. Since to be cited more is better, it is not sufficient to use the number of citations n, but its square n2, f = n2/W. This gives following progressions of the measure f:

number of citations directly in one line

2 2 1.33

3 3 1.5

4 4 1.6

n n 2n/(n + 1)

It is always better to have 2 citations directly, than infinite many citations in one line, since this means an oblivion.

Systems evaluated by scientometrics do not have any objective physical properties, therefore it is impossible to decide experimentally, which technique of evaluation or which measure is better than other ones. Their choice is based on mental arguments, only, or on authority of their supporters and on traditions.

It seems to be reasonable to demand, that criteria applied to scientometric results, which is based on techniques of linear algebra, be compatible with its multidimensionality and other characteristics.

The proposed measure f has some properties, which can be applied for solving some open problems. If indirect citations are counted, their effect is decreasing indirectly with the length k of branches f = 2n/(k + 1). Maybe, the second power at n has too great dumping effect on indirect citations. This power can not be less than 2, otherwise f of long indirect citations chains were lesser than 1, and it can not be greater than 2.58, since then a combination of one child with one grandchild would give greater f than two.

I used names of Euclides and Hilbert without corresponding items in references, supposing basic textbook knowledge. Citing a texbook has only low impact on the distance measure f of their long citation trees. Such permanent effects must be measured otherwise. Distances in citation trees could be suitable. W favors long chains.

It were possible to introduce time into a distance measure, counting distances between citations as time intervals. The impact factor is such a rough measure, based on a limit. It does not reckon with all descendants. Therefore W = n, the impact factor is qual to f. A high impact factor means fast direct citations. Even if seems that to remain long in the memory has its merits, mathematics is ruthless. Long live the impact factor!

1. M. KUNZ, Plots against information laws, Science and Science of Science, 3 (1-2) (1995) 91.

2. M. KUNZ, About metrics of bibliometrics, Journal of Chemical Information and Computer Science, 33 (1993) 193.

3. M. KUNZ, Distance matrices yielding angles between arcs of the graphs, Journal of Chemical Information and Computer Science, 34 (1994) 957.

4. Z. MIHALIC, D. VELJAN, D. AMIC, S. NIKOLIC, D. PLAVSIC AND N. TRINAJSTIC, The distance matrix in chemistry, Journal of Mathematical Chemistry, 11 (1992) 223-258.

5. M. KUNZ, On topological and geometrical distance matrices, Journal of Mathematical Chemistry, 13 (1993) 145.

6. M. KUNZ, An innovation of Schroedinger´s cat (in Czech), Chemické Listy, 87 (1993) 452.

7. R. ZAHRADNÍK, P. JUNGWIRTH, A note to the paper of Milan Kunz entitled "An innovation of Schroedinger´s cat" (in Czech), Chemické Listy, 87 (1993) 884.

8. M. AISSEN, B. SHAY, Numerical codes for operation trees, In Graph Theory and Its Applications: East and West, Capobianco, M. F.; Guan, M.; Hsu, D. F.; Tian, F., Eds., Annals of the New York Academy of Sciences, 1989, Vol. 576, 1.