|
|
|
Podivuhodný svět vektorů
Milan Kunz
Původní rukopis vznikl před počítačovou érou. Skener mi umožnil dostat článek do počítače a rozlišení bylo natolik dobré, že opravy nedaly zas tak mnoho práce.
Podnětem k napsání mi byl článek v aprílovém čísle nevím už kterého ročníku Vesmíru, který se dotkl problému konstrukce našeho vesmíru, zda je nejlepší z možných, jedině možný, či je to jenom jedna z nesčetných variant, která tak obdivuhodně vyhovuje některým lidem, že si troufají považovat tento svět za svůj, jakoby byl zhotoven na jejich objednávku. Odpovědi nelze hledat ve fyzice, která studuje jedinou v
ariantu vesmíru přístupnou našim smyslům a přístrojům, ale v matematice, která zná mnoho prostorů: Euklidovské a neeuklidovské, Riemanův, Hilbertův, Banachův, abychom jmenovali aspoň ty nejznámější.Sama matematika má mnoho oborů: algebru, analytiku, geometrii, topologii, logiku, kombinatoriku a ještě více teorií: čísel, informace, pravděpodobnosti, grafů, množin, her. Jednotlivé obory se rozvíjejí často zcela autonomně a navíc vůči fyzice či chemii má matematika pro chudé vědce jednu výhodu, i základní ob
jevy lze stále ještě dělat bez nákladných technických zařízeni, a jak dokázal brněnský rodák Goedel, počet těchto možných objevů je nekonečný, na rozdíl od fyzikálního vesmíru, který být nekonečný nemůže, ovšem pokud je správná současná interpretace rudého posunu světla (rychlost jeho rozpínáni by byla vyšší než rychlost světla, takže to nekonečno nemůžeme nikdy poznat). Descartes ukázal svou analytickou geometrii isomorfnost algebry a geometrie. Z jednotnosti matematických disciplin pak vyplývají zákonitosti prostorů, ve kterých může jakýkoliv vesmír existovat.Na počátku bylo slovo.
Co toto tvrzeni jedné autoritativní knihy znamená? Zvláště když si připomeneme jiné tvrzení, že všechno jsou jen slova, slova, slova.
Co vlastně jsou slova? Prostředek dorozumění mezi lidmi, iniciátory složitých biochemických procesů v našich mozcích, kterým říkáme myšlení, operátory transformující stav našeho vědomí, formující naše myšlenky jako desoxyribonukleová kyselina bílkoviny či pouhé sledy symbolů?
V každém případě dnes slova dala vzniknout celému polygrafickému průmyslu a internetu, psaním se živí statisíce lidí a touto autonomní produkcí se opět zabývá celá řada vědních oborů včetně matematiky.
Málokdo si však uvědomuje, v čem se svět slov podobá fyzikálnímu světu, že to prázdnota, která překvapila fyziky na přelomu tohoto století, když odhadli vzdálenosti, které dělí jádra atomů od elektronů. Jednotlivé jazyky uznávají jako slova jen asi milion kombinací písmen, ačkoliv lze vytvořit přes 2x10
11 kombinací písmen, které nejsou delší než 8 písmen. Jako slova využíváme jen asi miliontinu možných kombinací. To umožnilo vznik stovek autonomních světů jednotlivých jazyků, které mají často společných jen několik stejných kombinací hlásek s různým významem. Nebudeme dále sledovat všechny z toho plynoucí analogie a spokojíme se předpokladem, že na počátku bylo slovo a protože slovo je vektorem informace a my chceme vytvořit prostor, spojíme symboly písmena s vektory a vektorovým prostorem, symbolu j odpovídá jednotkový vektorej
(0, 0,.., 1j,. . 0n)v n rozměrném vektorovém prostoru.
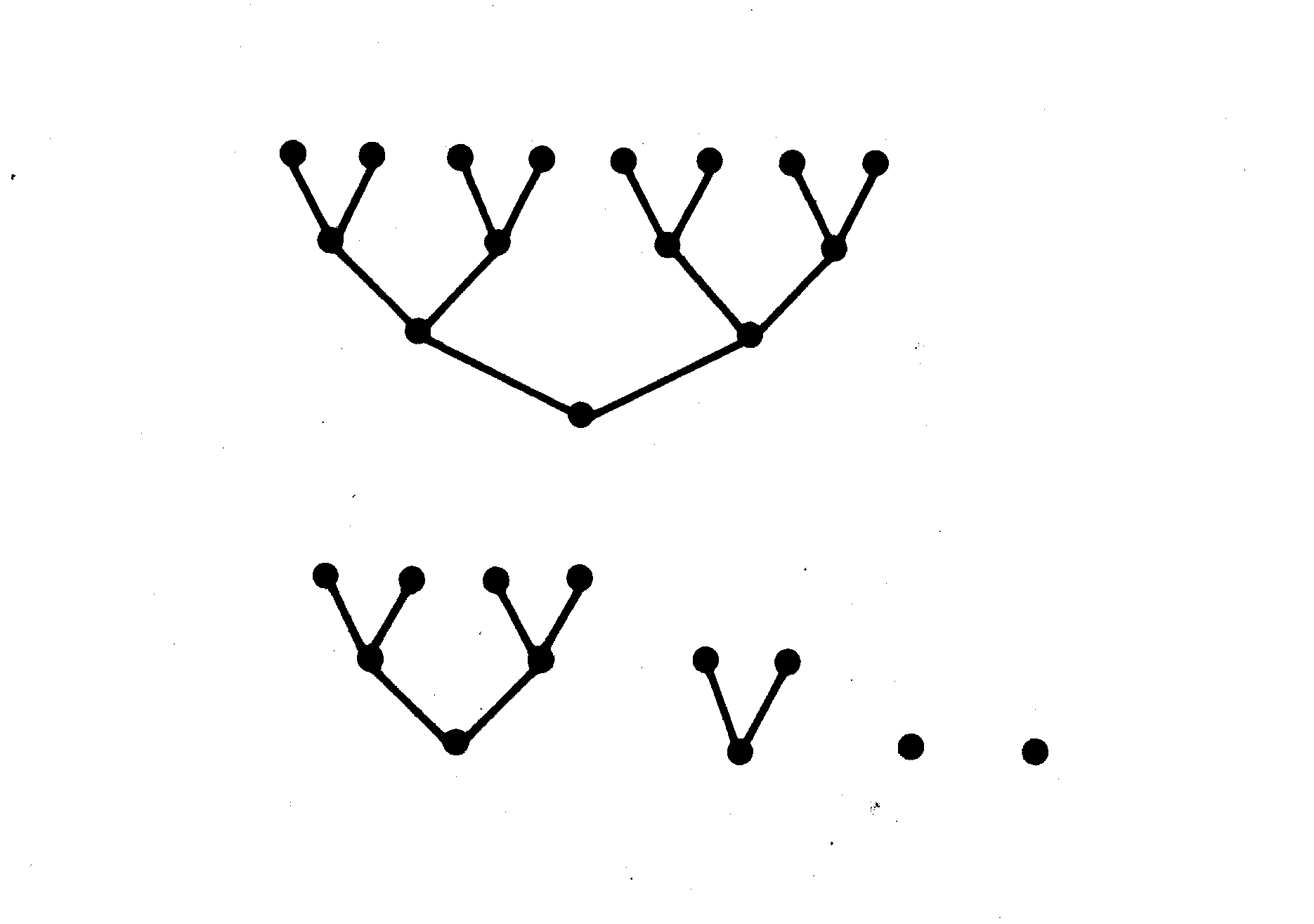
Předpokládá se, že jednotlivé vektory jsou navzájem kolmé, což nám činí potíže, protože si nedovedeme představit více rozměrů. V geometrickém prostoru, ve kterém jsme uloženi, dokážeme najít místo jen pro tři navzájem kolmé vektory. Nemusíme se tím problémem trápit, topologická sít tvořená vektory zůstane zachována i když své vektory složíme jako deštník. Ne nadarmo má v kombinatorice podobný postup název umbrella calculus (Obr. 1).

Obr. 1 Topologická sít vektorového prostoru. Síť cest vektorového prostoru nezávisí na úhlech, které jednotlivé vektory svírají. Zobrazeny jsou na jednoduchém přikladu dvojrozměrného prostoru též vliv velikosti úhlů mezi dvěma vektory.
Slovo si představíme jako sled pohybů v prostoru, které nás přenesou z počátku do určitého bodu v prostoru. A můžeme je nahradit jediným vektorem ukazujícím výsledek (Obr. 2).

Obr. 2 Rozdíl m
ezi slovem (sledem vektorů) a jeho výsledkem. Ze součtu sledu vektorů (b) nelze poznat v jakém sledu vektory byly původně uspořádány (a).V algebře tento rozdíl odpovídá rozdílu mezi nekomutativní a komutativní algebrou. V lingvistice rozdílu mezi textem knihy a jejím frekvenčním slovníkem. Z četnosti jednotlivých slov snad zjistíme, o čem kniha pojednávala, ale nedovíme se, jaké názory autor zastával. A ve fyzice? V tak zvaném fázovém prostoru prý můžeme ukázat stav soustavy jej i polohou, průvodičem. Je
stli na počátku bylo slovo, tak jsme pouhým určením výsledné polohy soustavy abstrahovali informaci obsaženou v uspořádáni jednotlivých částic tvořících soustavu, tato informace obsažená v původním sledu písmen se prostě ztratila, takže takový zjednodušený popis nemůže být úplný. Takové chyby se dopustila moderní fyzika při studiu mikročástic. Vycházela z faktu, že nám byly dostupné pouze statistické údaje o mikročásticích a že k statistickým operátorům neexistují operátory inversní. Z toho vyvodila, že mikročástice musí mít jiné vlastnosti než objekty přístupné přímo našim smyslům. Objevila se domněnka, že tyto částice jsou nerozlišitelné. Dnes ji ovšem vyvrací sama fyzika, která dokáže zobrazit jednotlivé atomy a registrovat jednotlivé elektrony a fotony.Lineární algebra
Zmínili jsme možnost, že symbol lze formálně ztotožnit s jednotkovým vektorem
ej a vektorovou řadu se slovem, jak však postupovat obráceně? Co například by znamenal zápis (1, 1, 0) nebo zápis (2, 0, 0)? V prvém případě oba vektory a i b působí simultánně, to znamená, že by měly znít současně, tvořit akord jako v hudbě různě vysoké tóny nebo hlasitost slova. Druhý případ lze geometricky těžko odlišit od následného působeni dvou jednotkových vektorů, může však znamenat působeni závaží o dvojnásobné specifické hmotnosti a ve slově dvojnásobnou intensitu hlásky, nikoliv její opakování (Obr. 3).
Obr.3 Různé možnosti působeni vektorů. a) Simultánní působeni jednoho nebo dvou vektorů. b) Následné působeni vektorů.
Musíme si stanovit pravidla pro operace se slovy, určit jakým způsobem budeme vektory sčítat, násobit a dělit. Nejprve si stanovíme, že pokud vektory působí současně, tak je sčítáme na jednom řádku, pokud působí po sobě, zapisuji se řádky za sebou analogicky se zápisem symbolů ve slově.
V Moliérově komedii je měšťák radostně překvapen, že mluví prózou. Podobně se budete asi divit i vy, když se dozvíte, že umíte násobit vektor sloupec
V jednotkovým vektorem řádkem JT. Prostě napíšete čísla do sloupce a sečtete je. Násobeni obecným vektorem je trochu složitější, nejdříve musíte vektor vážit, násobit vzájemně odpovídající čísla a pak teprve sčítat. Podobně se násobí i matice. S maticemi můžeme provádět i další matematické operace. Vedle obvyklého sčítáni, odčítáni a násobeni je můžeme také transponovat, což znamená že na vektor řádek se díváme jako na sloupec. Matice můžeme také obracet jako rukavice. K tomu se však vrátíme později. Nejprve si všimneme násobení. Nejprve toho případu této operace, kdy se nezmění charakter matice, pouze se jedno slovo transformuje na slovo jiné. Abychom toho dosáhli, musíme násobit jednotkovými maticemi, které mají jedinou jednotku nejen v řádcích, ale i sloupcích. Těmto maticím se říká permutační, protože permutují u matice M na kterou působí sloupce, pokud násobíme zprava MPn, nebo řádky, pokud násobíme zleva PmM. U textu odpovídá násobení zleva permutaci pořadí symbolů, násobeni zprava substituci jedněch symbolů druhými. Záměna písmen se používá při kódování zpráv, kdy nechceme, aby jim někdo jiný rozuměl, permutace lze také využít k tomuto účelu, ale lepší příklad je mechanická sazba. Z písmenek v sazečově kase je možné vysázet jakýkoliv text, pokud zásoba jednotlivých znaků stačí prostým vybíráním liter z jednotlivých přihrádek a jejich vkládáním do řádků. Prostým rozmetáním sazby můžeme postup opakovat a dostaneme zcela jiný text, který může mít zcela opačný význam.Matematicky jsou však všechny takto vznikající texty ekvivalentní. Množina všech permutačních matic
Pn tvoří grupu cyklických permutací Sn. Výsledek násobeni slova-naivní matice N zprava si můžeme představit jako rotaci na ploše v n-rozměrném euklidovském prostoru kolmé k jednotkovému vektoru In. Množina všech matic s m řádky a n sloupci zaplní všechny body tohoto prostoru s celočíselnými kladnými koordinátami, n-rozměrný plošný simplex. Abychom si mohli podobně představit permutace řádků, musíme přijmout předpoklad, že jednotka v jednotkovém vektoru ej označuje délku vektoru odpovídajícího příslušnému řádku, (délka je (j - 1) jednotek, abychom obsadili i nulové koordináty). Každé permutaci potom odpovídá bod v m rozměrné krychli.Mimo násobení permutačními maticemi můžeme násobit naivní matice jednotkovými vektory, sloupcem
J a řádkem JT (index T značí transposici vektoru ze sloupce na řádek a naopak).Při násobení sloupcem
NJn dostaneme vždy jednotkový vektor J, všechny matice se zobrazí do jednoho bodu v m-rozměrném prostoru. Při násobeni řádkem JT N dostaneme koordináty konečného bodu vektorové řady.A také můžeme násobit naivní matici
N její vlastní transponovanou maticí NT. Při tom dostaneme v případě NTN diagonální matici jejíž prvky jsou shodné s prvky matice JTN, pouze místo na řádku jsou zapsány na diagonále matice. V případě NNT jednotkové symetrické matice odrážející strukturu textu, jeho symetrii. U součinů JTN a NTN se celá operace scvrkává na pouhé počítáni počtu jednotek v jednotlivých sloupcích matice, což je operace značně triviální. Přesto se její pomoci podařilo rozřešit dva sporné problémy moderní vědy.Prvním je vztah dvou definic entropie H, Boltzmannovy Hn a Shannonovy Hm
H = -
Obě definice mají stejný tvar, ale pravděpodobnosti mají v obou definicích různý význam, Boltzmannova definice je spojena se symetrii sloupců matice
N, nebo matic JTN a NTN. Je to logaritmická míra symetrie orbity odpovídající danému rozděleni čísla (počtu kvant energie) m na n vektorů (počet částic). Shannonova entropie je logaritmickou mírou symetrie permutace symbolů textu, pokud použijeme logaritmy přirozené. Shannon však používá ve své definici logaritmy o základu 2. V tomto případě má jim definovaná entropie ještě jiný, názornější význam (viz Obr. 4).
Obr. 4 Interpretace informační entropie. Pro indexováni m prvků regulárním binárním kódem je potřeba m log
2 m symbolů. Po rozděleni prvků do n podmnožin postačí pro indexováni prvků S mjlog2mj prvků. Rozdíl je mírou informace o prvcích množiny. Kód: Vlevo 0, vpravo 1.Vzhledem k tomu, že základní symetrie slova je
PmNPn, jsou entropie (Hm + Hn) aditivní veličiny, což vysvětluje zcela jednoduše zdánlivou nadbytečnost informace pozorované v přirozených soustavách. Entropie Hm dosahuje maxima, když všechny symboly mají v textu stejnou četnost (frekvenci). V tomto případě je však Hn nulová, takže celková entropie není maximální. Hn by byla maximální, kdyby každý vektor měl svou četnost, což je však možné jen ve speciálních případech.Slova
i písmena nejsou v textech rozdělena rovnoměrně, jejich rozděleni není ani normální, ale extrémně kosé a podle momentu, který sledujeme, je známo jako Zipfovo, Lotkovo či Bradfordovo. Nejjednodušeji se modeluje jako useknuté logaritmicko normální rozděleni. Výhodou tohoto rozděleni je, že velice snadno z četnosti klíčových slov poznáme, o čem je řeč.Boltzmannovo řešeni maximální entropie molekul ideálního plynu vedlo k exponenciálnímu rozděleni tepelné energie molekul a normálnímu rozděleni jejich vzájemných rychlostí. U fotonů toto rozděleni energii neplatí, jejich rozděleni popisuje Bose-Einsteinova rovnice. Rozdíl se vysvětloval tím, že prý jsou klasické částice rozlišitelné a bosony nerozlišitelné. Tato interpretace vyvolala četné filosofické spory, k
teré dodnes neskončily.Ukázalo se však, že formální definice fyzikální nerozlišitelnosti
PnTNPn (stejná grupa symetrie působí na matici z obou stran) je v rozporu s definici nerozlišitelnosti buněk podle klasické kombinatoriky, počet diagonálních vektorů je stejný jako počet řádkových vektorů JTNPn.Je těžko pochopit, proč k oběma nedorozuměním vůbec došlo, když základní principy Boltzmann jasně formuloval a jedná se o zcela elementární jednoduché počty. Asi proto, že Boltzmann sám považoval kvantovou domněnku a číselný přiklad ji dokládající za pouhou berličku, kterou odhodil, jakmile formuloval příslušné integrály. Boltzmann použil hypotézu o existenci kvant energie třicet let před Planckem bez fyzikálních důkazů. V té době ještě nebyly Riemannovy názor
y o vlastnostech diferencovatelných funkci běžné, lineární algebra teprve vznikala a pochopeni významu symetrie pro fyziku se teprve rodilo. Těžko říci, zda by pomohlo, kdyby Boltzmann své úvahy zobecnil pomoci úplné indukce.Entropie a ji odpovídající fun
kce H byly považovány za mlhavé a špatně definovatelné pojmy, které lze libovolně používat. Použití terminu entropie navrhl Shannonovi Norbert Wiener, to pak vedlo k mnoha zcestným úvahám o tom, že informace je jakýmsi opakem fyzikální entropie, negentropií. Tyto hypotézy jsou nyní hluboce zakořeněné.Nemohu si zde odpustit osobní vzpomínku. Zabralo mi to 18 měsíců intensivního studia, než jsem mohl dokázat, že entropie, Boltzmannova a Shannonova, jsou nejen rozdílné funkce, ale dokonce funkce aditivní. Když jsem napsal publikaci, byla mi vrácena, protože prý za a) odporuje všemu, co stoji v učených knihách, za b) je nesrozumitelná. To mne naštvalo tak, že jsem ji přepsal pro časopis Věda a technika mládeži, kde vyšla. Redaktorovi se můj způsob výkladu asi
zdál natolik jasný, že předpokládal, že jej pochopi i mladí čtenáři.V jiném případě recensent namítal Maxwellova démona, který prý může snižovat entropii soustavy ideálního plynu tím, že třídí molekuly na rychlé a pomalé. Odpověděl jsem mu článkem, ve kterém analyzuji činnost démona, který nejprve míchá rozdělené molekuly, čímž entropii soustavy zvyšuje a teprve pak, aniž jakkoliv změní svou činnost, molekuly třídí. Vycházel jsem ze zkušenosti socialistické společnosti, která nás nutila vykonávat zbytečn
ou práci, zaměstnávajíc nás činnostmi, které jinak probíhají samovolně.Vztah mezi démonovou informaci a entropii není tedy jednoznačný. Článek o démonovi sice v časopise vyšel, ale recensenta jsem nepřesvědčil a tak matematická práce byla časopisem zamítnuta bez rozboru matematických důkazů.
Grafy
Těžko lze odhadnout, zda by se historie vědy odvíjela jinak, kdyby v Athénách bylo 7 mostů jako v Královci a kdyby si peripatetikové na svých procházkách místo studia dokonalých těles položili otázku, zda je možné přejít všechny mosty jenom jednou. Vždyť ani Euler si neuvědomil význam jaký teorie grafů nabude. Grafy jsou objekty sestávající z n vrcholů a m vztahů mezi vrcholy. Tyto vztahy se obvykle znázorňuji jako hrany spojující jednotlivé vrcholy. Vztah může
být symetrický, hrana je neorientovaná, nebo nesymetrický, kdy je hrana orientovaná. Pro náš výklad postačí znát pojem úplného grafu, v kterém existuje (n2 - n)/2 hran mezi všemi vrcholy grafu spojitého, v kterém neexistuje žádný izolovaný vrchol a grafu acyklického, ve kterém hrany netvoří žádný cykl.Nejmenším spojitým a současně největším acyklickým grafem je strom s (n - 1) hranami.
Začali jsme s vektorovými prostory a jednotkovými vektory
ej. Jaký je vlastně vzájemný vztah graf a vektorů? Představme si orientovaný graf s (n+1) vrcholy v němž všechny hrany vycházejí z vrcholu O a dostaneme graf - hvězdu. Vektoru o dvojnásobné délce odpovídá dvojnásobná hrana, Orientovaný graf lze definovat jako rozdíl dvou naivních matic, neorientovaný jako jejich součet. Hraně v tom případě odpovídá vektor kolmý na tuto hranu, což však není na závadu, protože se jedná jen o názorné zobrazení.
Obr. 5. Úplné grafy se 4 a 5 vrcholy. Jsou to současně 4 a 5-rozměrné plošné sim
plexy.Čtyřstěn si velice snadno představíme, protože je to třírozměrné těleso. Horší je to, pokud se pokusíme nalézt bod, který by byl stejně vzdálen od všech vrcholů a ležel mimo danou plochu. To znamená, že nemůže být uvnitř simplexu, leda bychom využili čas a simplexem pohnuli. Nejsme schopni si v trojrozměrném prostoru představit, jak na sebe jednotlivé trojrozměrné řezy čtyřrozměrným prostorem přiléhají, pokud si to nepředstavíme jako proces v čase.
5-rozměrný simplex je omezen 5 čtyř-rozměrnými plochami, což jsou čtyřstěny, které můžeme identifikovat jen postupně, nejprve ABDE a BCDE a potom ABCD, ABCE, ACED, protože se nám v našem prostoru překrývají.
S grafy můžeme spojit matice. Pro náš výklad budou důležité incidenční matice orientovaného grafu
Ssij
= -1, jestliže hrana i vychází z vrcholu j,sij
= 1, jestliže hrana i končí ve vrcholu j,sij
= 0 v ostatních případech.Matice neorientovaného grafu G
gij
= 1, jestliže neorientovaná hrana i je incidentní s vrcholem jgij
= 0 v ostatních případech.Matice sousedství grafu A
aij = 1 vrchol i je spojen s vrcholem j hranou,
aij
= 0 v ostatních případech.Platí A = 1/2 [GTG - STS
] (za předpokladu, že prvky G a S se liší jen znaménky).Matice vzdálenosti D
dij = počtu hran na spojité cestě mezi vrcholy i a j.
Matice cest W je definovaná jen pro stromy jako wij = 1, hrana j leží na cestě i mezi dvěma vrcholy stromu.
Mezi n vrcholy existuje n(n-l)/2 cest, proto má matice W stejně tolik řádků.
Proč je člověk mírou všech věcí
Z klasické liter
atury jsou známy sentence, že vše má svou míru a člověk je mírou všech věcí, pokusíme se objasnit, proč tomu tak je a proč naopak pro vztahy mezi lidmi jsou důležité peníze, majetek, věci nebo třeba společné myšlenky.
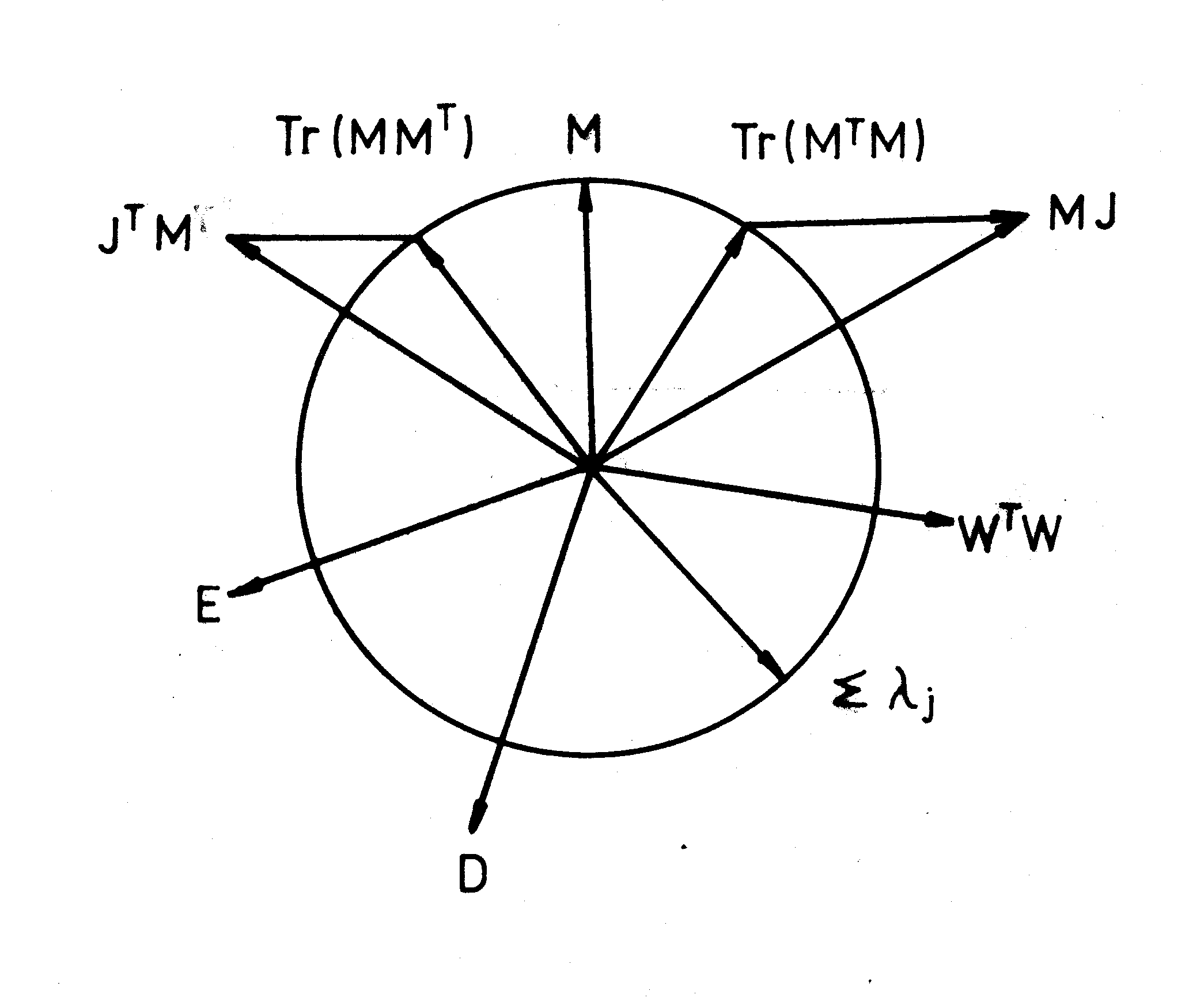
Obr. 6. Vektor matice M
a jeho průměty do prostoru sloupců a řádků. Stopy Tr kvadratických forem MTM a MMT jsou stejně dlouhé jako vektor matice M a vektor vlastních hodnot těchto kvadratických forem S l j. K těmto vektorům se druží vektory inversních matic vnějších i vnitřních. V případě že M = S stromu, E je Eichingerova matice, D je matice vzdáleností a WTW je kvadratická forma matice cest W. Vektor SJ v tom případě má nulovou délku, Tr(STS) a mimodiagonální prvky tvoří smyčku.Tak tedy p
ředpokládejme, že existuje společný prostor věcí a lidí a vztahy mezi těmito věcmi a lidmi. Dejme tomu, že věci jsou vědecké publikace a vztahy mezi prostoru odpovídá matice M jejímiž prvky jsou mij = 1, jestliže osoba j je autorem nebo spoluautorem publikace i, mij = 0, jestliže se nejedná o autora. Můžeme vše komplikovat, když budeme vážit podíly jednotlivých autorů na výsledné publikaci, můžeme dokonce i uvažovat o negativních zásluhách určitých osob na vzniku publikace.Dalším krokem bude to, že si společný prostor rozdělíme, vytvoříme separátní prostor věci a separátní prostor lidi. Docela jednoduše to uděláme tak, že matici
M vynásobíme zprava jednotkovým vektorem sloupcem J nebo zleva jednotkovým vektorem řádkem JT. To je zcela jednoduché, sečteme prvky matice v jednotlivých sloupcích (obdobně s J v jednotlivých řádcích).Co jsme udělali? Podívejme se znovu na Obr. 6.
Matice M
představuje ve společném prostoru lidi a věci vektorovou řadu, jejíž Euklidovskou délku zjistíme tak, že sečteme čtverce všech prvků matice ML2 = S mij2
Tomuto vektoru odpovídají dva polohové vektory, jeden v prostoru věcí
MJ a jeden v prostoru lidi JTM. Prvky vektoru v prostoru publikací jsou autoři, u každé publikace počítáme, kolik má autorů. Prvky v prostoru lidí jsou publikace, autory hodnotíme dle toho, kolik mají publikací.Jak zjistíme délku vektoru? Tím, že najdeme jeho kvadratickou formu, tedy
JTMMTJ pro prostor sloupců a JTMTMJ pro prostor řádků. Nás budou zajímat jádra těchto kvadratických forem MTM a MMT, jejich orámováni jednotkovými vektory jenom sečítá prvky matice do jednoho čísla.Když si provedeme násobeni oběma způsoby podle pravidel platných v lineární algebře, zjistíme, že na diagonály obou kvadratických forem se promítají součty čtverců prvků matice
M, stopy, jak se říká součtu diagonálních prvků matice, stejně dlouhé jako vektorová řada M. Leží tedy ve vektorovém prostoru na kouli, mimodiagonální prvky tvoří spolu se stopou odpovídající projekci JTM či MTJ pravoúhlý trojúhelník. (Ten může degenerovat i na přímku). Pokud vycházíme z matic, které obsahuji jen jednotkové prvky, potom se na diagonále kvadratických forem objeví počty prvků jednotlivých vektorů. Mimodiagonální prvky ukazují, kolik prvků mají dva vektory společné. Kdybychom kvadratické formy normalizovali, deformovali je tak, aby na diagonále se objevily vždy jen jednotky, potom by se společné prvky mohly považovat za míry úhlů mezi dvěma vektory. Prostor kvadratických forem je znám jako Hilbertův. Je to vlastně Euklidovský prostor, ve kterém se nestaráme příliš o to, o kolikarozměrný prostor se vlastni jedná, všechny vektory se sklopí do jedné roviny.S Hilbertovým prostorem se setkáváme ve fyzice, ale nyní stále více ve faktorové analýze a jiných statistických metodách, kde se to nijak nezdůrazňuje a nevysvětluje.
Cílem faktorové analýzy je nalézt vlastni vektory - faktory a vlastni hodnoty kvadratické formy. Co to vlastně je? Představme si vektorovou soustavu jako jakýsi polarizační filtr, kterým pozorujeme daný objekt. Při otáčeni filtru objekt střídavě zjasňuje a ztemňuje. Při určitém nastavení soustavy objekt zcela zprůhlední. U matice odpovídají zjasňovací a ztemňovací změny velikosti prvků matice. Při zprůhledňováni se mimodiagonální prvky zmenšuji a stahuji k hlavni diagonále, pás nenulo
vých prvků se zužuje kolem hlavní diagonály, až nakonec se soustředí jen na diagonále. V tom okamžiku jsme našli vlastni hodnoty matice, její řešení. Protože součet vlastních hodnot se rovná stopě matice, jsou vektory obou kvadratických forem stejně dlouhé jako původní vektorová řada.S touto matematickou operací lze srovnat myšlenkové procesy. Snaha pochopit problém dlouho nevede k cíli, až najednou, v jednom vzácném okamžiku je vše jasné, jednotlivé kameny mosaiky zapadnou na svá místa a my jasně vidíme všechny souvislosti a faktory ovlivňující problém.
Moebiusova inverse
Snad každý zná Moebiusovu pásku, která má jediný povrch, ačkoliv vzniká z listu o dvou površích stočením a slepením. Méně známá je Moebiusova funkce z teorie čísel, kde je inversi k Erasthotenovu sítu dělitelů čísla n.
Vezměme matici, jejímiž prvky jsou 1, jestli číslo i je dělitelné číslem j (i
ş 0 mod j), jinak 0. Inversní matice k této matici má prvky -1, jestliže i/j je prvočíslo nebo součin lichého počtu prvočísel, 1, jestliže i/j je součin kladného počtu prvočísel, 0, jestliže i/j je dělitelné čtvercem prvočísla a jindy.Pojem Moebiusova inverse byl rozšířen v kombinatorice na všechny případy uplatněni principu inkluse a exkluse i na diference. Vzhledem k tomu, že všechny tyto případy lze zapsat v maticové formě, je přirozené vztáhnout tento pojem na všechny inversní matice. lnverzní matici je matice
F, pro kterou platíFlM = I
v tomto případě se jedná o inversní matici zleva, nebo
MFr
= Ikde Fr je inversní matici zprava. V některých případech existují obě inversní matice a v tom případě jsou shodné. Nezbytnou podmínkou pro existenci inversní matice je, aby invertovaná matice nebyla singulární, což znamená,že matice nemá žádný nulový vektor. Nebo jinak řečeno, matice musí mít nenulový determinant, součin jejích vlastních hodnot nesmi být nulový. Tento požadavek pochopíme, jestliže si uvědomíme, že vlastni hodnoty inversní matice jsou obrácené vlastní hodnoty původní matice. Teď bychom měli používat limity, stačí však říci, že v tom případě by musela být stopa inversní matice nekonečně veliká, takže inversní matice přestává být dobře definovaná.
Proč nás inversní matice zajímají? To souvisí s charakterem úloh, který musíme řešit. Dejme tomu, že známe vektor příčin x a operátor, který změní příčiny v následky y. Operátor má formu matice M. Pak snadno můžeme vypočítat vektor y
y = Mx.
Ve fyzice často stojíme před inverzní úlohou. Známe výsledky působeni fyzikálních sil
y, z teorie matici M a chceme určit fyzikální sily, které výsledek vyvolaly. Potomx
= M-1y.Stromy poznání
V posledních desítiletích pociťujeme stále tíživěji důsledky informační exploze, nezvládnutelný exponenciální růst počtu vědeckých publikací. Mnozí vkládají naděje do strojových informací, kdy pracné a zdlouhavé hledání informací za nás udělají stroje, které už jsou schopny hledat v úplných textech. Následující příběh, který začal už v idylických poválečných dobách, musí být varováním před přílišným optimismem. Týká se prakticky jednoho vědního oboru. Vědci, kteří v oboru pracovali, se vzájemně znali, když ne osobně, tak určiti znali své práce. Nikoho však nenapadlo konfrontovat výsledky, i když se jednalo o pouhé kupecké počty.
Jedna linie je spojena s fyzikální chemií, mechaniko
u pohybu polymerních řetězců, viskositou jejich roztoků. Jejího řešení se zúčastnila celá řada autorů a vývoj byl spojen s řadou nedorozumění, která byla způsobena tím, že obě kvadratické formy matice lineárního řetězce STS a STS jsou si značně podobné:STS
|
1 |
-1 |
X |
0 |
0 |
|
-1 |
2 |
X |
0 |
0 |
|
X |
X |
X |
X |
X |
|
0 |
0 |
X |
2 |
-1 |
|
0 |
0 |
X |
-1 |
1 |
SST
|
2 |
-1 |
X |
0 |
0 |
|
-1 |
2 |
X |
0 |
0 |
|
X |
X |
X |
X |
X |
|
0 |
0 |
X |
2 |
-1 |
|
0 |
0 |
X |
-1 |
2 |
Obě matice se liší jen dvěma rohovými prvky a rozměrem,
STS má n řádků a sloupců, SST má o jeden řádek a sloupec méně.Navíc je tu diference matice
¶ STS, která má vynechaný prvý řádek a sloupec¶
1STS|
2 |
-1 |
X |
0 |
0 |
|
-1 |
2 |
X |
0 |
0 |
|
X |
X |
X |
X |
X |
|
0 |
0 |
X |
2 |
-1 |
|
0 |
0 |
X |
-1 |
1 |
která se liší od matice SST pouze v jediném prvku.
Tento jediný prvek má dramatický vliv na tvar inverzní matice line
árního řetězce (¶ 1STS)-1|
1 |
1 |
1 |
1 |
.. |
|
1 |
2 |
2 |
2 |
.. |
|
1 |
2 |
3 |
3 |
.. |
|
1 |
2 |
3 |
4 |
.. |
|
.. |
.. |
.. |
.. |
.. |
Matice STS
je singulární a už Kirchhoff dokázal, že má vždy jednu nulovou vlastní hodnotu. Její hlavní podmatice s vynechaným řádkem a sloupcem, jako je ¶ STS mají tedy inverzní matici, která je diferenci inverzní matice (SST)-1. Její tvar nalezl Rouse a vlastní hodnoty této matice odpovídají relaxačním dobám pohybu polymerního řetězce.Druhá strana vývoje je spojena se jménem jmenovce zakladatele kybernetiky Wiene
ra, který měl směšné křestní jméno Harry. Harry si v roce 1947 všimnul, že body varů alkanů lze korelovat se součtem vzdálenosti mezi všemi uhlíkovými atomy molekuly. Wienerův index byl jedním z prvních v celé řadě tak zvaných topologických indexů, které nalezly v posledních letech značné uplatnění v organické chemii, zvláště v souvislosti s hledáním nových léčiv. Pohybují se na hranici mezi empirickými vztahy a kvantovou chemii. Jednoduše vypočtené indexy v řadě případů s dostatečnou přesností nahrazuji kvantově mechanické výpočty, které pro složité molekuly nejsou stále rutinní záležitostí. V nikterých případech se již podařilo nalézt pro některé topologické indexy teoretické vysvětlení.U Wienerova indexu, který byl považován za úměrný součtu prvků matice vzdálenosti, to bylo jednoduché jako Kolumbovo vejce: stačilo si všimnout, že stopa Rousovy matice je shodná s Wienerovým indexem lineárního řetězce. Ostatní už byla technická záležitost. Ukázat, že Rousova matice je totožná s kvadratickou formou
WTW matice cest W a dokázat že tyto matice existuji pro všechny stromy. A tak jsou aplikace Wienerova indexu podloženy teorii. Dokonce se ukázalo, že zlom v lineární závislosti teploty varů lineárních alkanů na Wienerovu indexu koresponduje se zlomem závislosti integrační konstanty pro náhodný let lineárních molekul, vypočtený Guptou a Eichingerem už skoro před 20 lety. Tím však proces poznáni nekončí. Ukazuje se, že matice stromů lze svinout podobni jako to udělal Moebius se svou páskou, takže nepoznáme, co je vně a co je uvnitř. Kvadratická forma WTW je inverzí kvadratické formy SST incidenční matice stromu(WTW)SST = I.
Když si najdeme druhou kvadratickou formu
WWT, snadno zjistíme, že její diagonální prvky jsou vzdálenosti mezi jednotlivými vrcholy stromu, jsou tedy shodné s prvky matice vzdáleností D. Tuto matici získáme z diagonály matice WWT metodou jejímž autorem je Eichinger. Diagonální vektor převedeme na čtvercovou matici tím, že ji vynásobíme z obou stran incidenční matici úplného grafu SkSkT(Diag WWT)Sk = D - D
kde D je diagonální matice součtu vzdálenosti vrcholů v grafu vůči ostatním. A teď přijdou překvapení, za která by se nemusel stydět ani Houdini, kdyby se věnoval matematickým trikům. Platí totiž vztah
STDSTT = I
matice vzdálenosti je vnitřní inversní matici incidenční matice stromu
ST. Vysvětlení, proč tyto vztahy platí pouze pro stromy je poměrně jednoduché. Gordon se spolupracovníky ukázal, že stromy tvoří bázi vektorového prostoru úplných grafů. Ale to ještě není všechno. Eichinger definoval matice E transformující kvadratickou formu úplného grafu SKSKT v matici WLWLT, která se rovněž uplatňuje v statistické mechanice polymerních řetězců. Z formalismu těchto matic plyne vztahSTESTT = I.
Eichingerovy matice jsou současně vnitřními inversními maticemi incidenčních matic stromů. Eichingerovy matice souvisí také se vzdálenostmi ve stromech. Přímo se získají jako součet inversních matic všech n diferencí matice
d jSTTSTE =
S (d jSTTST)-1Diference matice
d jSTTST je matice STTST s vynulovaným j-tým sloupcem a řádkem.Skutečnost, že mikročástice se někdy chovají jako částice, jindy jako vlny vyvolala v dvacátých letech mnoho filosofických diskusí a spory o interpretaci Schroedingerovy rovnice, zda jsou mikročástice lokalizovány, dosud neskončily. Tady jsme si ukázali čtyři ekvivalentní popisy objektů se strukturou stromů, které se navíc dají vyjádřit nekonečnými součty goniometrických funkcí.
Několik problémů
Nevím, jak by se uvedené výsledky líbily starořeckým filosofům, ale zdá se mi fascinující, že tak složité fyzikální vlastnosti, jako je teplota varu alkanů, plynou jen z čistě matematických vztahů, diskrétnosti a struktury molekul.
Nevím, proč fyzikové nevysvětluji žákům, že základní principy zachováni energie, hmotnosti, jsou ekvivalentní tvrzení, že se soustava pohybuje po rovině v mnohorozměrném Euklidovském prostoru. Shora uvedené vztahy by měly být platné, jak lze dokázat úplnou indukcí, pro libovolně velké soustavy. Lze si tedy představit, že na počátku byl vesmír ve stavu, kdy veš
kerá energie byla soustředěna do jednoho vrcholu energetické plochy, a od velkého třesku padá do orbit, kde má stále bohatší symetrii. V orbitě s maximální entropii může uváznout. Pokud se bude vracet zpět, s pravděpodobností hraničící s jistotou se nevrátí do výchozího vrcholu, ale do některého vrcholu jiného.Mnohem zajímavější je však jiná implikace. Na příkladě stromů jsme si ukázali, že nelze říci, co je vlastně vně a co je uvnitř. A pokud si uvědomíme algoritmus, podle kterého se počítají prvky inversních matic, zjistíme, že izolované objekty mají jiné inversní matice a tedy vlastnosti než objekty zařazené do všech souvislosti a navíc, že každý prvek inversní matice závisí na hodnotách všech ostatních prvků matice. Abychom použili našeho přikladu, inv
ersní vlastní hodnota autora závisí na tom, jak jsou rozděleny publikace mezi ostatními autory. Ovšem tato hodnota má pouze statistický význam, protože uvedené matice nijak neváží význam jednotlivých publikací, jsou uměle vytrženy z daleko širších matic. Nakonec chci předejít možné kritiky a prozradit vady na kráse dané koncepce. Je sice dokázána ekvivalence maticového zápisu kvantové mechaniky a Schroedingerových vlnových funkci, ale problematické je pokoušet se popsat celý vesmír jedinou maticí. Protože každá změna prvků matice musí vést ke změně inversní matice, mohou mít docela malé změny nepředvídaně velké důsledky (příkladem jsou uvedené matice lineárního řetězce). Otázka zní, jakým způsobem vlastně soustava své inversní matice hledá. Pokud tento proces není okamžitý, ale je tvořen náhodnými změnami, jak to předpokládá mechanika polymerních řetězců, potom vztahy ve fyzikálním vesmíru nemohou být tak ideální, jak jsme je předvedli.Slovo, které jej tvoři, je příliš dlouhé. Jeho čtení nám zabírá čas. Mezitím se to, co jsme přečetli i to, co se chystáme číst stále mění.
Literatura
S leností sobě vlastní odkazuji na seznam publikací na této stránce. V nich jsou všechny odkazy.